Zapisovanie množiny reálnych čísel pomocou intervalov
V článku Množina a jej určenie, konečná a nekonečná množina sme si hovorili o dvoch možnostiach zápisu množín – vymenovaním prvkov alebo určením charakteristických vlastností prvkov. Pozrime sa teraz spoločne na nasledovné dve zadania:
Príklad 1:
Dané sú dve množiny: A = {x∈N; 2<x<7}, B = {x∈R; 2<x<7}. Zapíšte tieto množiny vymenovaním prvkov.
Riešenie:
Množinu A viete určite všetci zapísať vymenovaním prvkov bez zaváhania. Teda A = {3; 4; 5; 6}.
Čo ale spravíme s množinou B? Bude to tiež množina {3; 4; 5; 6}?
Určite nie, pretože by sme museli zapísať i číslo 2,1 alebo 2,23 alebo 2,2346 alebo 2,007 atď. pretože všetko sú to reálne čísla väčšie ako 2 a zároveň menšie ako 7. Správne uvažujete, že vymenovaním prvkov sa nám množinu B nepodarí zapísať. Vždy by sme našli ďalšie a ďalšie čísla, ktoré by neboli zapísané.
A riešenie?
Množina B patrí medzi tie množiny reálnych čísel, ktoré je možné zobraziť na číselnej osi úsečkou, polpriamkou alebo priamkou, pričom krajné body tejto úsečky alebo začiatočný bod polpriamky môžu, ale nemusia patriť k týmto množinám. Takéto podmnožiny množiny R nazývame intervaly .
Ohraničené intervaly sú intervaly, ktoré je možné na číselnej osi zobraziť pomocou úsečky. Podľa toho, či tejto úsečke patria 2, 1 alebo žiadny z krajných bodov rozlišujeme ohraničené intervaly uzavreté, polouzavreté a otvorené .
| Interval | Množina | Znázornenie na číselnej osi | Zápis |
|---|---|---|---|
| uzavretý | {x∈R; a≤x≤b} |  |
<a, b> |
| (zľava uzavretý, sprava otvorený) | {x∈R; a≤x<b} |  |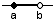
<a, b) |
| polouzavretý (zľava otvorený, sprava uzavretý) | {x∈R; a<x≤b} |  |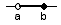
(a, b> |
| otvorený | {x∈R; a<x<b} |  |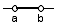
(a, b) |
A teraz môžeme zapísať množinu B z príkladu 1 ako interval (2; 7).
Pri zápise neohraničených intervalov používame znak + ∞ alebo – ∞.
| Interval | Množina | Znázornenie na číselnej osi | Zápis |
|---|---|---|---|
| sprava neohraničený | {x∈R; x≥a} |  |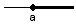
<a, ∞) |
| {x∈R; x>a} |  |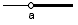
(a, ∞) | |
| zľava neohraničený | {x∈R; x≤a} |  |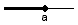
(-∞, a> |
| {x∈R; x<a} |  |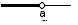
(-∞, a) | |
| obojstranne neohraničený | R |  |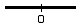
(-∞, ∞) |
Keďže intervaly sú množiny, tak môžeme určovať zjednotenie, prienik, rozdiel intervalov i doplnok intervalu vzhľadom na množinu R.
Príklad 2:
- Dané sú intervaly A = <–2, 3), B = (–1, 5>, C = (3, ∞). Určte
- a) A∪B
- a) A∩B
- a) C – B
- b) B‘R
Riešenie:
a)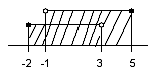 
A∪B = <-2; 5>
b)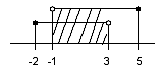 
A∩B = (-1; 3)
c)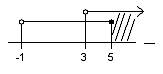 
C – B = (5; ∞)
d)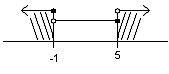 
B‘R = (-∞; -1> ∪ (5; ∞)