Exaktná matematika a geometria – podobne ako prírodné vedy – boli v dnešnom chápaní vzdialené mezopotámskemu človeku. Nemožno mu to však zazlievať. História pokroku ešte nebola motorizovaná a hospodárske či spoločenské potreby ho nenútili myslieť rýchlejšie. Ešte nepotreboval techniku, ktorá by ho viedla k unáhlenému tempu pokusov. Sumer bol človek čisto praktický. Zoznámil sa s číslami a s ich používaním, lebo si to od neho vyžadovalo hospodárenie na pôde. Prejavovalo sa to v účtovníckej agende, najmä pri palácovom či chrámovom hospodárstve, ku ktorej sa priraďovalo zememeračstvo.
Záznam matematických poznatkov sa zachoval na hlinených tabuľkách formou klinového písma. Niektoré symboly boli rovnaké pre viacero čísel – ich význam rozoznali buď podľa polohy v čísle alebo z kontextu úlohy.

S rátaním si Sumeri vedeli poradiť rovnako ako dnešný prváčik. Rátali na prstoch, a tak sa dostali k číslu 10 – k základu decimálnej sústavy. V ďalšom rátali až do 60 ( ako naši predkovia na kopy ). Najskôr preto, že číslo 60 je najnižšou spoločnou mierou viacerých deliteľov. Preto sa toto číslo používalo pri delení roka na dni alebo pri delení kruhu na stupne. V začiatkoch sa Sumeri nad toto číslo nedostali. Na rozdiel od Babylončanov a Asýrčanov, ktorí mali znak pre číslo 100 (
me
) aj pre číslo 1000 (
lim
), Sumeri museli používať znakovú kombináciu. Pre číslo 100 kombináciu 60 + 40 a pre číslo 1000 ( 60 + 40 ) + 40.
Sumerskí počtári rozdelili deň na 12 dvojhodín a každú dvojhodinu na 30 dielov. Deň sa v novobabylonskom období začínal od polnoci. Učenec, ktorý prišiel s touto novinkou sa volal Kidinnu ( Grékmi nazývaný Kidinas ). Dospeli aj k rozdeleniu kruhu a ekliptiky na úseky s dvanástimi dvojhodinami, čím vznikol zvieratník, v ktorom každému znaku prináleží 30 stupňov.
Desiatková i šesťdesiatková sústava poskytovala možnosť realizovať všetky počtárske úkony. Zostavili aj tabuľky so súpismi násobenia podľa vzoru: 2 x 1 = 2, 2 x 2 = 4, 2 x 3 = 6 …až do 2 x 20, 2 x 30 a 2 x 50. Aj delenie malo svoj zaznačený systém: nikdy sa neuvádza delenec, teda 2/3 = 40, 1 = 30, 1/3 = 20. Z toho vyplýva, že delenec bol 60.
[adinserter block=“1″]Na zaznačovanie zlomkov sa používali osobitné znaky, no iné v praktickom živote a iné v teoretickom vyjadrení. Poznali aj druhé a tretie odmocniny, vypracované takisto v tabuľkách.
Všetky tieto pomôcky predstavujú vlastne „
najstaršie zbierky príkladov z matematiky
. Učitelia počtov bývali dôležitými členmi učiteľských zborov na mezopotámskych školách. Pričinili sa o rozmach matematiky a vied, ktoré sa o ňu opierajú. Už v sumerskej epoche sa prepracovali k rovniciam s jednou či dvoma neznámymi a položili tak základy algebry, ktorá predpokladá vysoký stupeň aritmetických vedomostí. Babylonskí matematici riešili rovnice – aj kvadratické a sústavy rovníc. Neexistovali algebraické výrazy – rovnice boli zapísané slovne. Vo výpočtoch prišli dokonca na podstatu Ludolfovho čísla. Svoje π vyjadrili veľmi približne číslom 3. Preto dnes znalci o Sumeroch vyhlasujú, že sa práve v matematike dopracovali ku skutočnej virtuozite.
Rovnaké úspechy mali geometri. Priviedla ich k nim potreba merať ( a po záplavách vždy znova premeriavať ) parcely polí, záhrad, pastvín … Hranice medzi nimi bolo treba vyznačovať kolíkmi. Tým sa už v druhej polovici 3. tisícročia zamestnával osobitný úradník rabi sikkati ( náčelník kolíkov ), so svojím štábom. Vyhotovoval katastrálne plániky parciel s podrobným označením ich rozmerov. Pri parcelách nepravidelného tvaru sa žiadalo, aby sa v plánikoch vyskytovali obdĺžniky aj trojuholníky. Zachoval sa skutočný kataster celého kraja Charránu ako podklad na stanovenie pozemkovej dane.
Medzi mnohými geometrickými úlohami, ktoré obsahuje séria príručiek z 18. str. pred n. l., sa zachovala aj jedna osobitne ťažká pre žiakov babylonských škôl: „
Vypočítaj uhlopriečku obdĺžnika so šírkou 10 a dĺžkou 20 lakťov!
“ Úlohu vyriešili, a priblížili sa tým k princípu, ktorý oveľa neskôr vyjadrovala Pytagorova veta. Podobne objavili aj jadro Euklidovej vety.
Príklad v reči Babylončanov (sar = jednotka obsahu, sila = jednotka objemu):
„
Z 30-tich sarov som zobral 20 silov zrna. Z druhých 30-tich sarov som zobral úrodu 15 silov zrna. Úroda prvého poľa bola o 8,20 väčšia ako úroda druhého. Obsahy oboch polí sú dovedna 30. Aké veľké sú polia?
“
Zapísané v dnešnej symbolike:
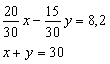
Utvorenie sústavy mier a váh treba nepochybne priznať už Sumerom. Názvy niektorých jednotiek hovoria o dávnom pôvode a súčasne dokladajú konkrétny spôsob myslenia. Ich hodnota nebola konštantná, menila sa podľa času a miesta.
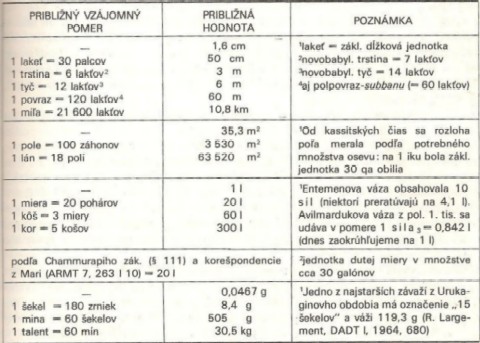
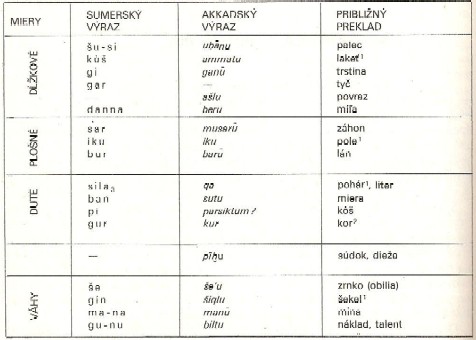
Dĺžkovou mierou sa stal lakeť, ale aj „trstina“. Výška budov v Asýrii sa merala počtom radov tehál, základnou plošnou mierou bol starobabylonský záhon, konštantou dutých mier sa stal desaťsilový obsah Entemenovej striebornej vázy. Najmenšou jednotkou hmotnosti bolo zrnko. Presnejší prehľad mier a váh je uvedený v tabuľke.
Autor: Mária Hanulíková
Zdroje:
Josef Klíma, Ľudia mezopotámie
