Objem trojbokého hranola

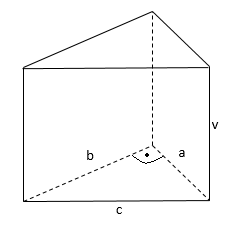
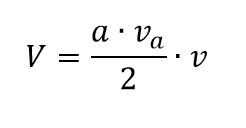Hranol je teleso, ktoré má dve rovnako veľké a tvarovo zhodné podstavy, ktoré sú spojené rovnobežnými bočnými stenami. Keďže podstava hranola je v tomto prípade trojuholník, výpočet objemu hranola je trošičku náročnejší ako pri hranoloch s podstavou v tvare obdĺžnika.

Výpočet objemu hranola s podstavou trojuholníka pozostáva z dvoch krokov:

• Výpočet obsahu podstavy – trojuholníka.
• Vynásobenie obsahu trojuholníka výškou hranola (vzdialenosťou medzi týmito dvoma podstavami).

Výpočet plochy trojuholníka:

Obsah trojuholníka môžeme vypočítať jednej zo strán trojuholníka a prislúchajúcej výšky napr. nasledovne:

S = (a ⋅ v_a) / 2

Pozrite sa v nasledovnom prehľade na ďalšie spôsoby výpočtu obsahu trojuholníka – obsah trojuholníka vzorec.

Výpočet objemu hranola:

Keď už poznáme obsah jednej z podstáv, môžeme vypočítať objem hranola, ktorý je daný ako súčin obsahu podstavy a výšky hranola:

V = S_p . v

Kde:

Obsah podstavy je (a ⋅ v_a) / 2, pričom a predstavuje dĺžku strany trojuholníka a v_a predstavuje prislúchajúcu výšku.
v predstavuje výšku hranola, teda vzdialenosť medzi oboma podstavami.

Objem trojbokého hranola – príklady

Peter si kúpil netradičné akvárium v tvare trojbokého hranola. Podstava je tvorené pravouhlým trojuholníkom s odvesnami 30 cm a 40 cm, výška akvária je 80 cm. Koľko litrov vody bude v akváriu, ak ho Peter chce naplniť do 3/4 výšky?

a = 30 cm = 3 dm
b = 40 cm = 4 dm
v = … 3/4 z výšky akvária … = 3/4 . 80 cm = 3 . 20 (lebo 80:4=20) = 60 cm = 6 dm
V = ? dm³ = ? l

Obsah pravouhlého trojuholníka vypočítame ako polovicu súčinu odvesien – ab/2

V = S_p . v
V = (a.b)/2 . v
V = (3.4)/2 . 6
V = 36 dm³ = 36 l

V akváriu bude 36 litrov vody.

---

Robotníci vykopali rigol v tvare trojbokého hranola. Aká je dĺžka rigola, ak vykopali 168 m³ zeminy a prierez rigola tvorí trojuholník so stranou 1,6 m a prislúchajúcou výškou 1,4 m?

a = 1,6 m
v_a = 1,4 m
V = 168 m³
v = ? m

S_p = (a ⋅ v_a) / 2 = (1,6 . 1,4) / 2 = 1,12 m²

V = S_p . v
168 = 1,12 . v ……. /:1,12
150 m = v

Robotníci vykopali rigol s dĺžkou 150 metrov.

Ďalšie zaujímavé príklady nájdete aj na stránke Objem a povrch kvádra a kocky – príprava na Testovanie 9