Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. https://www2.nucem.sk/dl/5874/ZAK23008_S_TZ-RT-Mat-SJ-fA_1000.pdf Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
Monitor 2024 matematika
1. príklad
Zadanie:
Zásoba uhlia na vykurovanie 15 domácností vystačí na 60 dní. Na koľko dní vystačí rovnaká zásoba uhlia, ak sa pripojí k vykurovaniu ešte päť domácností? Predpokladáme, že všetky domácnosti majú rovnakú spotrebu.
Riešenie:
Zápis:
15 domácností …… 60 dní
15+5=20 domácností … x dní
20 ⋅ x = 15 ⋅ 60
20x = 900 /:20
x = 45
Odpoveď: 45
2. príklad
Zadanie:
Peter si kúpil akcie zahraničnej firmy v celkovej sume 3 000 €. Dnes je ich hodnota o 50 % nižšia. O koľko percent musí od dnes stúpnuť cena týchto akcií, aby sa ich celková hodnota dostala opäť na pôvodných 3 000 €?
Riešenie:
dnes …….. 50% z 3000 = 0,5 ⋅ 3000 = 1500 € = základ, čiže 100%
keďže sa pýtame, o koľko percent od dnes musí stúpnuť cena akcií, aby sa dostali na hodnotu 3000 €, tak budúcich 3000 € bude pôvodných 100% + pridaných x%
100% …….. 1500 €
(100+x)% …. 3000 €
Použijeme krížové pravidlo:
100 ⋅ 3000 = (100+x) ⋅ 1500
300 000 = 150 000 + 1500x /-150 000
150 000 = 1500x /:1500
100% = x
Odpoveď: 100
3. príklad
Zadanie:
Deviataci riešili rovnicu: 0,1 ∙(8x + 3) = 0,5x – 0,6
V triede sa vyskytlo 5 rôznych výsledkov, korene: –1; –3; –0,3; –12 a „rovnica nemá riešenie“. Ich percentuálne zastúpenie je znázornené v kruhovom diagrame. Vyrieš rovnicu a pomocou diagramu zisti, koľko percent žiakov nemalo správny výsledok.
Riešenie:
Najskôr vyriešime rovnicu:
0,1 ∙(8x + 3) = 0,5x – 0,60,8x + 0,3 = 0,5x – 0,6 / -0,5x – 0,3
0,3x = -0,9 / :0,3
x = -3
Z grafu je zrejmé, že 20% žiakov malo správny výsledok.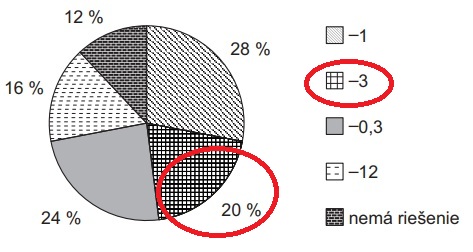
Odpoveď: 80
4. príklad
Zadanie:
Na tanieri je 12 buchtičiek, z toho 5 makových a 7 lekvárových. Koľko tvarohových buchtičiek k nim treba pridať, aby pravdepodobnosť, že náhodne vybraná buchtička bude maková, bola 20 %?
Riešenie:
Pravdepodobnosť vypočítame ako „počet priaznivých / počet všetkých“.
V našom prípade:
pravdepodobnosť …………………………20% = 0,2
počet priaznivých je počet makových buchtičiek … 5
počet všetkých možností …………………….. 12 + x, kde x je počet pridaných buchtičiek
Zostavíme rovnicu:
Pravdepodobnosť = počet priaznivých / počet všetkých
0,2 = 5 / (12+x) /⋅(12+x)
0,2 ⋅ (12+x) = 5
2,4 + 0,2 x = 5 / – 2,4
0,2x = 2,6 / :0,2
x = 13
Odpoveď: 13
5. príklad
Zadanie:
Ak z obdĺžnika so stranami dlhými 8 cm a 6 cm odstrihneme štyri zhodné trojuholníky tak, ako je znázornené na obrázku, dostaneme kosoštvorec. Koľko centimetrov meria obvod tohto kosoštvorca?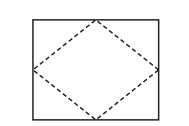
Riešenie:Získať prístup k riešeniu príkladov
Odpoveď: 20
6. príklad
Zadanie:
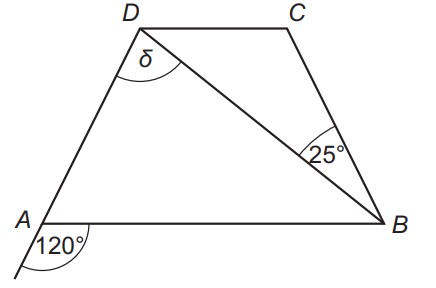
Na obrázku je znázornený rovnoramenný lichobežník ABCD. Vypočítaj veľkosť uhla δ. Výsledok uveď v stupňoch.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 85
7. príklad
Zadanie:
Na obrázku je znázornená sieť štvorbokého hranola s podstavou v tvare kosodĺžnika, ktorého strany majú dĺžku 30 cm a 20 cm. Vypočítaj objem tohto hranola. Výsledok uveď v kubických decimetroch.

Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 14,4
8. príklad
Zadanie:
Pavlína išla s rodičmi na zber jahôd. Hmotnosť debničky, do ktorej zbierali jahody, bola 550 g. Po ukončení zberu mala debnička spolu s jahodami hmotnosť 4,8 kg. Kilogram nazbieraných jahôd stál 2,80 €. Koľko eur zaplatili za nazbierané jahody bez debničky? Výsledok uveď s presnosťou na desatiny.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 11,9
9. príklad
Zadanie:
Mierka mapy je 1 : 50 000. Koľko kilometrov v skutočnosti meria trasa, ktorá má na tejto mape dĺžku 8 cm?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 4
10. príklad
Zadanie:
Hracia plocha šachovnice má 8 x 8 hracích polí. Koľko percent hracích polí je obsadených figúrkami na začiatku šachovej partie, ak obaja šachisti obsadia svojimi figúrkami dva rady?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 50
11. príklad
Zadanie:
Žiaci istej školy nosia rovnošatu: čierne nohavice a farebné tričko. Farba trička môže byť modrá, zelená, fialová, oranžová alebo tyrkysová. Tričko môže byť buď farebné bez pásikov, alebo farebné s tromi bielymi alebo s tromi čiernymi pásikmi. Koľko tried najviac môže byť v škole, ak žiaci jednej triedy majú rovnaké tričká a žiaci rôznych tried majú rôzne tričká?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 15
12. príklad
Zadanie:
Igor premieňal jednotky obsahu a objemu.
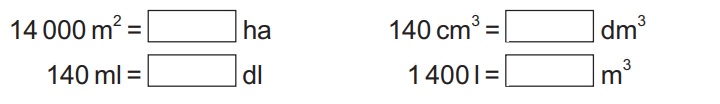
Správne doplnil všetky chýbajúce čísla a zistil, že okrem jedného príkladu doplnil vždy to isté číslo. Uveď číslo, ktoré sa líšilo od ostatných.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 0,14
13. príklad
Zadanie:
Jeden diel stavebnice v tvare kvádra má rozmery 3 dm, 2 dm a 1 dm. Deti postavili z týchto dielov v rohu miestnosti stavbu znázornenú na obrázku. Koľko dielov použili?.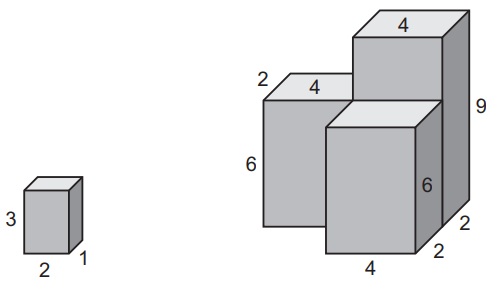
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 28
14. príklad
Zadanie:
V istom meste ukončilo športové gymnázium spolu 120 hokejistov, ktorí sa po ukončení štúdia profesionálne venovali hokeju. Aritmetický priemer ich mesačných platov vo veku 21 rokov bol 2 700 eur. Najvyšší príjem 200 000 eur mesačne mal hokejista, ktorý uspel v zahraničí. Vypočítaj priemerný mesačný plat ostatných hokejistov. Výsledok zaokrúhli na celé eurá.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 1 042

Na zadanie Spoločenské tance sa vzťahujú úlohy 15 a 16
15. príklad
Zadanie:
Na základe informácií z diagramu zisti počet respondentov, ktorí uviedli, že tango vedia tancovať čiastočne.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 380
16. príklad
Zadanie:
Na základe údajov uvedených v diagrame rozhodni, ktoré z uvedených tvrdení je nepravdivé.
A: Čaču vie tancovať čiastočne 29 % opýtaných.
B: Štvrtina opýtaných uviedla, že nevie vôbec tancovať.
C: Viac ako 75 % opýtaných vie tancovať valčík čiastočne alebo výborne.
D: Džajv vie tancovať výborne alebo čiastočne viac ako štvrtina opýtaných.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C

17. príklad
Zadanie:
Koľko stromov môžu poliať z nádoby, v ktorej je 1 m³ vody, ak na poliatie jedného stromu potrebujú 10 litrov vody? O strate vody pri polievaní neuvažujeme.
určite
A: 10 000
B: 1 000
C: 100
D: 10
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
18. príklad
Zadanie:
Keďže slnečné žiarenie poškodzuje plasty, nádoby sa zakrývajú plachtami, ktoré chránia bočné steny a hornú podstavu nádoby. Pomocou rozmerov uvedených na obrázku vypočítaj plochu plachty, ktorá zakrýva nádobu.
A: 4,4 m²
B: 5,6 m²
C: 5,8 m²
D: 6,8 m²
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
19. príklad
Zadanie:
Dopravná značka Chodník pre chodcov má tvar kruhu s priemerom 7 dm. Približne koľko decimetrov štvorcových plechu je potrebných na jej zhotovenie? Počítaj s hodnotou π = 3,14.

A: 22,0 dm² B: 38,5 dm² C: 44,0 dm² D: 154 dm²
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
20. príklad
Zadanie:
Oliver sledoval v sobotu v televízii historický dokument, ktorý trval 90 minút, v nedeľu si pozrel detektívny film dlhý 120 minút a počas pracovných dní si pozrel šesť častí fantasy seriálu, pričom každá časť mala 30 minút. V ktorej možnosti diagram zobrazuje správne rozdelenie minút medzi jednotlivými televíznymi žánrami, ktoré Oliver sledoval v televízii?

Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
21. príklad
Zadanie:
Ktoré z uvedených čísel je väčšie ako 1 milión a zároveň menšie ako 10 miliónov?
A: 2 ⋅ 107
B: 4 ⋅ 106
C: 6 ⋅ 105
D: 8 ⋅ 104
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
22. príklad
Zadanie:
Ktorý z výrazov M = 3x + 7, N = –x + 4, O = 2x – 8, P = –6x + 5 sa rovná súčtu ostatných troch výrazov?
A: M = 3x + 7
B: N = –x + 4
C: O = 2x – 8
D: P = –6x + 5
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
23. príklad
Zadanie:
Ktorou číslicou treba nahradiť *, aby bolo číslo 76*0 deliteľné dvomi, tromi, štyrmi a piatimi bezo zvyšku?
A: 4
B: 5
C: 6
D: 8
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
24. príklad
Zadanie:
Vrchol kocky je bod, ktorý je spoločným bodom troch stien kocky. Kocka na obrázku má zvýraznený jeden z vrcholov. V ktorej možnosti je znázornená sieť tejto kocky?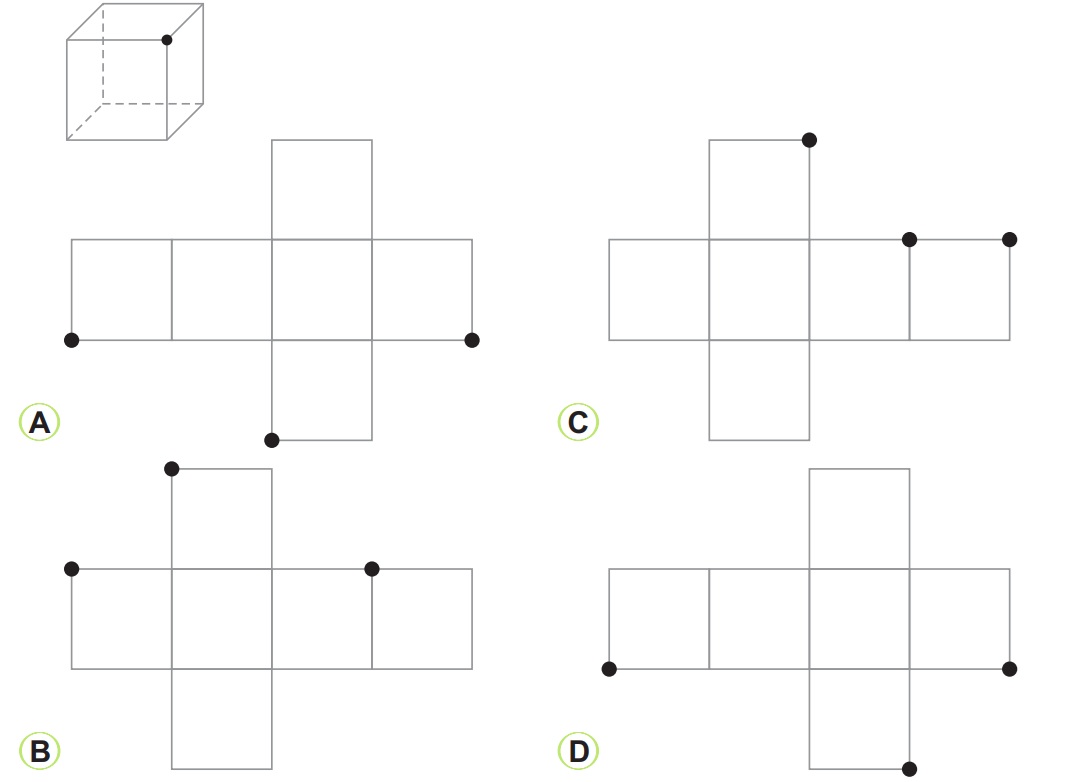
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
25. príklad
Zadanie:
Súrodenci Lea a Tomáš sa rozprávajú o svojich úsporách:
Lea: Ak by som mala o štvrtinu eur viac ako teraz, mala by som toľko ako ty.
Tomáš: Ak by som ja mal o pätinu eur menej ako teraz, mal by som toľko ako ty.
Ktorá z nasledujúcich možností je na základe ich tvrdení pravdivá?
A: Lea má teraz 400 eur a Tomáš 500 eur
B: Lea má teraz 400 eur a Tomáš 480 eur
C: Lea má teraz 480 eur a Tomáš 400 eur
D: Lea má teraz 500 eur a Tomáš 400 eur
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: A
26. príklad
Zadanie:
Stará mama pečie palacinky podľa tohto receptu: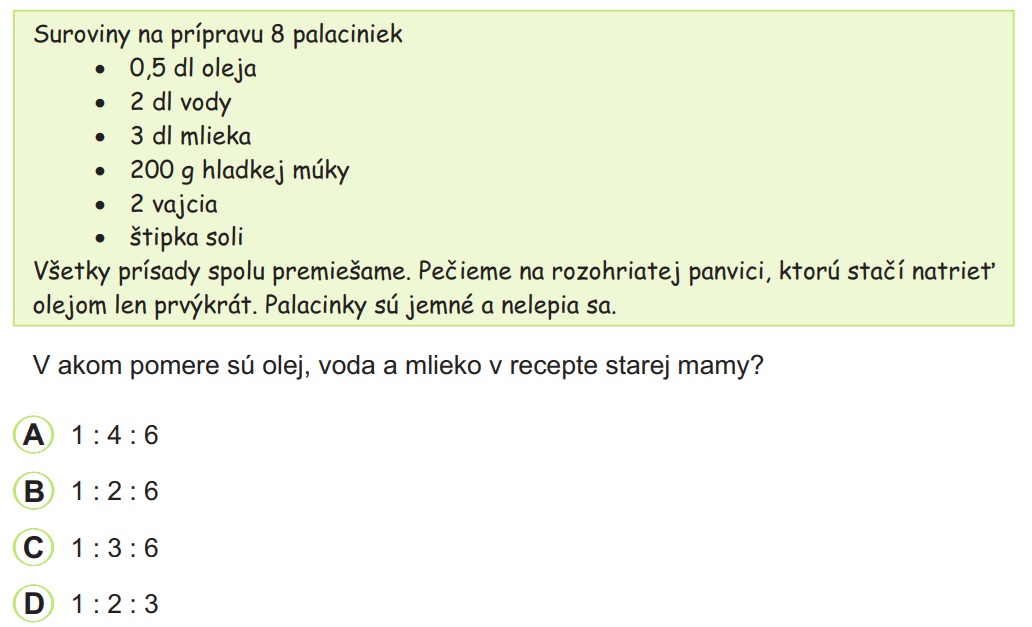
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: A
27. príklad
Zadanie:
Tabuľka uvádza vybrané druhy mlieka a ich zloženie.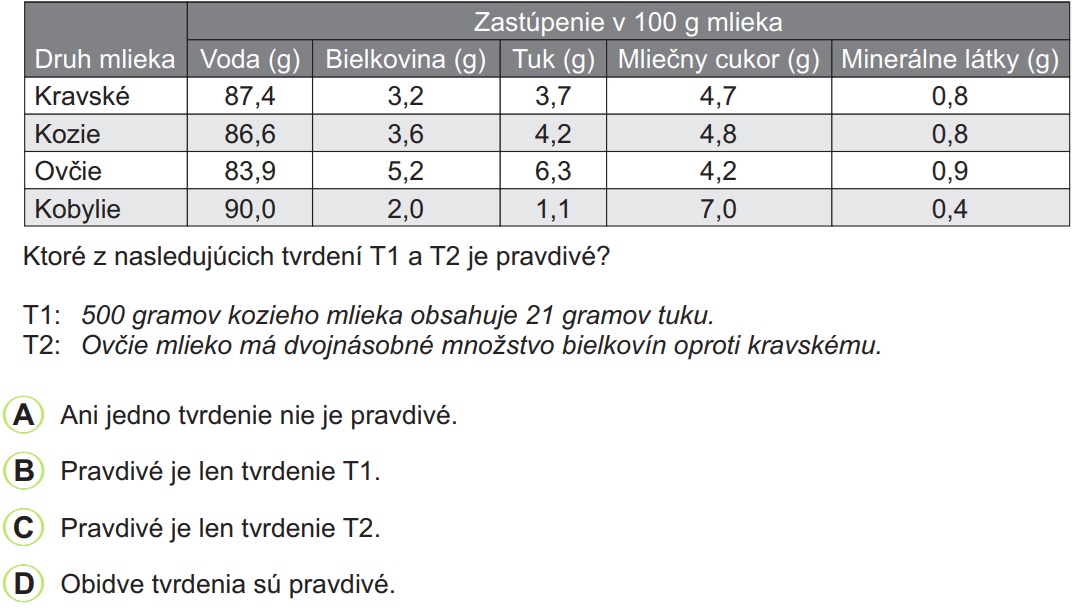
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
28. príklad
Zadanie:
Graf zobrazuje výsledky 12 súťažiacich v dvoch atletických disciplínach: v hode kriketovou loptičkou a v behu na 60 m. Deti sa kvalifikovali prekročením stanoveného limitu.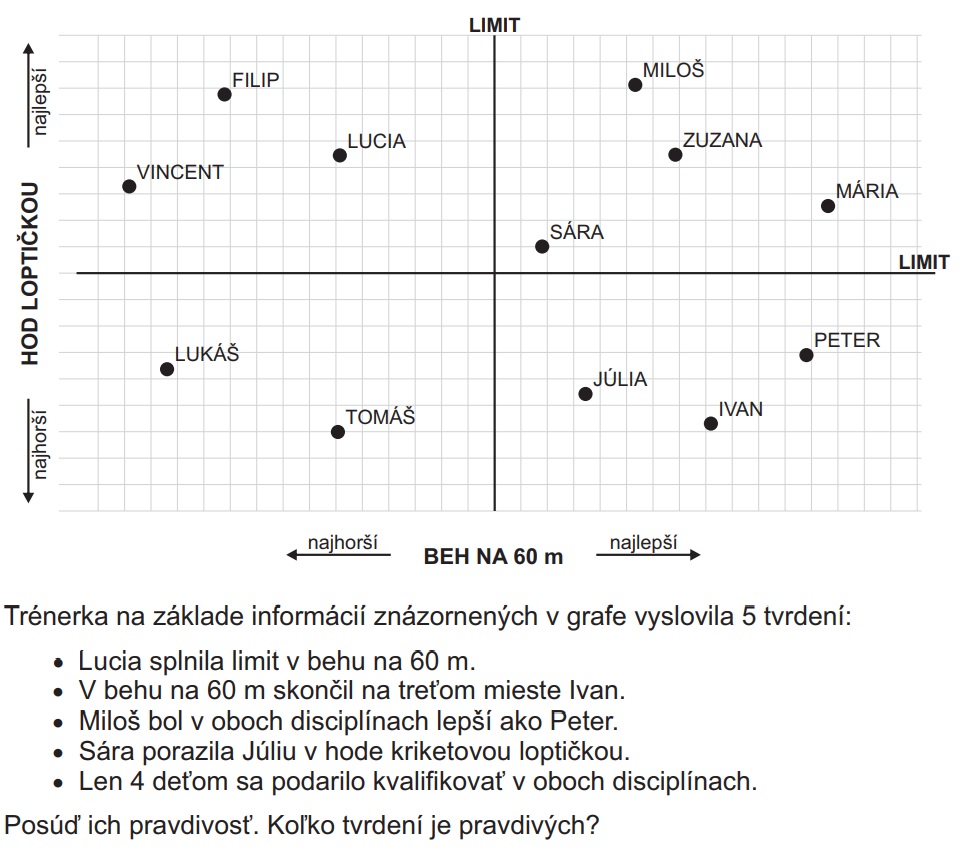
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
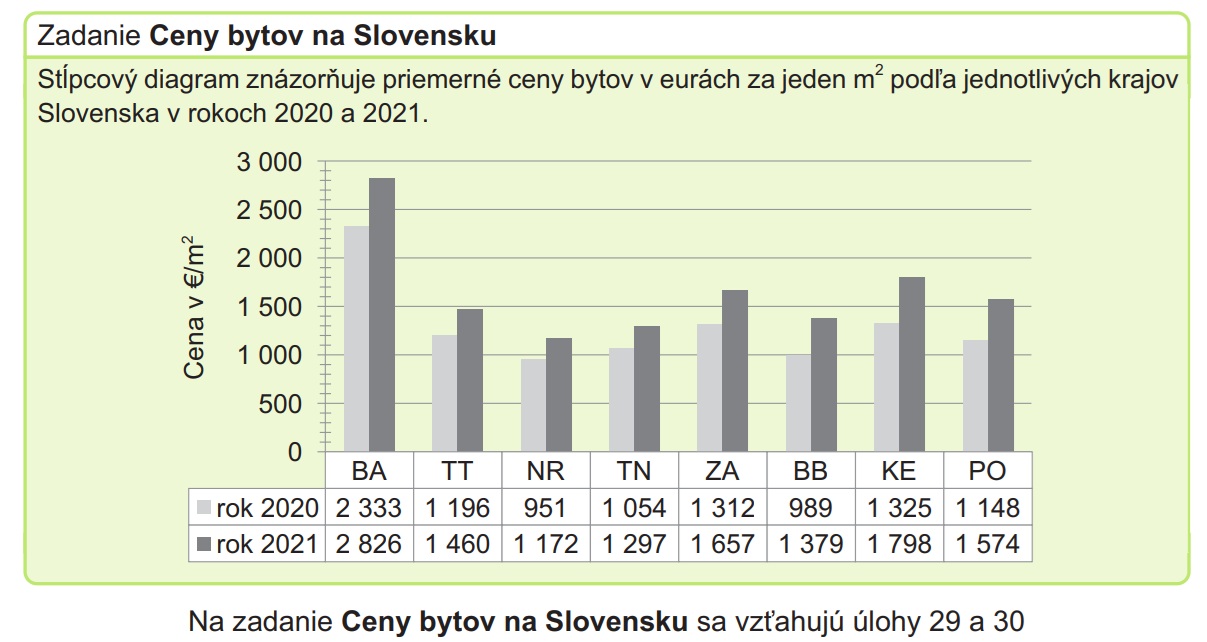
29. príklad
Zadanie:
O koľko eur stúpla priemerná cena bytu s rozlohou 55 m v roku 2021 oproti roku 2020 v kraji s najnižšou priemernou cenou bytov za jeden meter štvorcový?
A: 12 155 B: 13 365 C: 14 585 D: 15 735
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: A
30. príklad
Zadanie:
V ktorom z uvedených štyroch krajov stúpla priemerná cena bytov za 1 m² v roku 2021 oproti roku 2020 o viac ako 39%?
A: v Bratislavskom(BA)
B: v Žilinskom (ZA)
C: v Banskobystrickom (BB)
D: v Trenčianskom (TN)
Riešenie: Získať prístup k riešeniu príkladov
