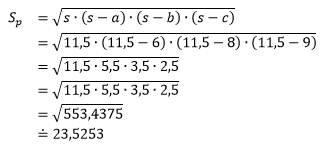Kolmý 3-boký hranol – vzorce, výpočet objemu

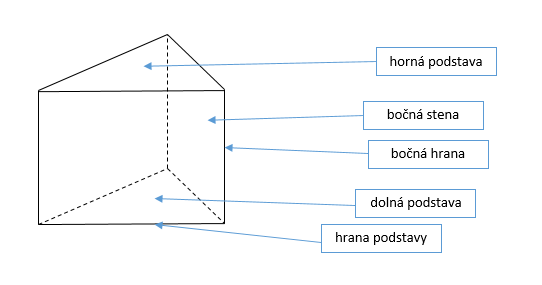
Kolmý 3-boký hranol je priestorový útvar s trojuholníkovou podstavou, pre ktorý platí:

• podstava je trojuholník;
• bočné steny sú kolmé na podstavu;
• bočné steny majú tvar štvorca alebo obdĺžnika;
• bočné steny hranola tvoria plášť;
• vzdialenosti podstáv hovoríme výška;

Popis trojbokého kolmého hranola:

S – povrch hranola, V – objem hranola, S_p – obsah podstavy, S_pl – obsah plášťa, a, b, c – hrany podstavy, v – výška hranola, o – obvod podstavy

Objem 3-bokého hranola (objem hranola s podstavou trojuholníka):

V = S_p . v, pričom na výpočet obsahu podstavu využijeme vzťahy pre výpočet obsahu trojuholníka.

Vzťahy na výpočet obsahu trojuholníka nájdete na stránke https://pohodovamatematika.sk/trojuholniky-vzorce.

Povrch 3-bokého hranola (povrch hranola s podstavou trojuholníka):

S = 2 . S_p + S_pl

Obsah plášťa vypočítame nasledovne: S_pl = o . v, kde o je obvod podstavy a v je výška hranola.

 

Vzorový príklad – hranol s podstavou všeobecného trojuholníka:

Vypočítajte objem a povrch hranola s výškou 8 cm a podstavou v tvare trojuholníka so stranami 6 cm, 8 cm a 9 cm.

Riešenie:

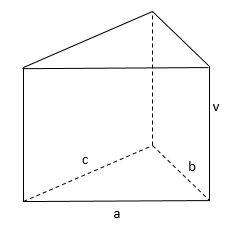
a = 6 cm
b = 8 cm
c = 9 cm
v = 8 cm
V = ? cm³
S = ? cm²

V = S_p . v

Na výpočet S_p využijeme Herónov vzorec, keďže ide o všeobecný trojuholník.

Najskôr vypočítame obvod trojuholníka: o = a + b + c = 6 + 8 + 9 = 23

Následne polovičný obvod: s = o : 2 = 11,5

A samotný obsah podstavy:

Zostáva už len vypočítať objem hranola:

V = 23,5253 . 8 = 188,2024 cm³

S = 2 . S_p + S_pl

S = 2 . 23,5253 + o . v = 47,0506 + (6 + 8 + 9) . 8
= 47,0506 + 184 = 231,0506 cm²

Vzorový príklad (hranol s podstavou pravouhlého trojuholníka):

Vypočítajte objem a povrch hranola s výškou 4,5 cm a podstavou v tvare pravouhlého trojuholníka s odvesnami 5 cm a 6 cm.

Riešenie:

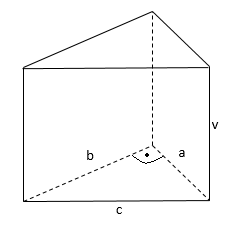
a = 3 cm
b = 4 cm
v = 4,5 cm
V = ? cm³
S = ? cm²

V = S_p . v

Obsah pravouhlého trojuholníka vypočítame ako polovicu súčinu jeho odvesien (odvesny v pravouhlom trojuholníku sú na seba kolmé), preto

S_p = (a . b)/2 = (3 . 4)/2 = 12/2 = 6 cm²

Potom V = S_p . v = 6 . 4,5 = 27 cm³

S = 2 . S_p + S_pl

S = 2 . 27 + o . v = 54 + o . 4,5

Aby sme mohli vypočítať obvod podstavy, potrebujeme zistiť dĺžku strany c. Využijeme Pytagorovu vetu:

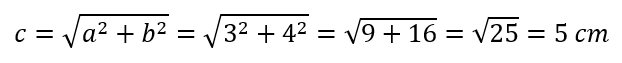
S = 54 + o . 4,5 = 54 + 5 . 4,5 = 54 + 22,5 = 76,5 cm²