Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
Monitor 2023 matematika
1. príklad
Zadanie:
V sčítacej pyramíde sa súčet čísel v susedných políčkach nachádza v políčku nad nimi. Ktoré číslo patrí v nasledujúcej sčítacej pyramíde na miesto otáznika?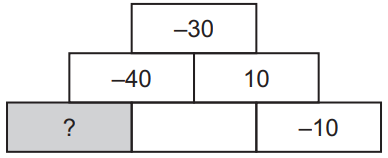
Riešenie:
Označme si neznáme číslo susediace s otáznikom premennou x. Keďže súčet čísel v susedných políčkach sa nachádza v políčku nad nimi, tak musí platiť:
x + (-10) = 10
Vzniknutú rovnicu ľahko vyriešime:
x + (-10) = 10
x – 10 = 10 /+10
x = 20
Keďže už poznáme číslo v políčku vedľa otáznika, vieme si zapísať ďalšiu rovnosť:
? + 20 = -40
A riešime:
? + 20 = -40 /-20
? = -60
Odpoveď: -60
2. príklad
Zadanie:
Priemerná spotreba automobilu je 5,6 litra paliva na 100 kilometrov. Koľko litrov paliva sa pri priemernej spotrebe minulo, ak automobil prešiel 800 km? Výsledok uveď s presnosťou na desatiny.
Riešenie:
V tomto prípade ide o priamu úmernosť, čím viac kilometrov automobil prejde, tým väčšia bude spotreba paliva.
5,6 l …….. 100 km
x l …….. 800 km
5,6 ⋅ 800 = x ⋅ 100
4 480 = 100x /:100
x = 44,8 l
Odpoveď: 44,8
3. príklad
Zadanie:
Na obrázku je znázornený úložný box v tvare kvádra s rozmermi 42 cm, 24 cm a 24 cm vyplnený zhodnými kockami. Koľko kociek je spolu v úložnom boxe, ak v hornej vrstve vidíme 28 kociek?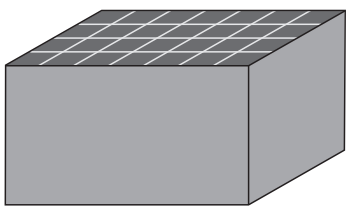
Riešenie:
Pri pohľade zhora vidíme, že na dlhšiu hranu, šírku boxu (42 cm) sa „zmestí“ 7 kociek a na kratšiu (24 cm) 4 kocky. Keďže aj výška boxu je 24 cm, tak na výšku to budú tiež 4 kocky.
Počet kociek si môžeme predstaviť ako rozmer kvádra – 7 kociek x 6 kocky x 4 kocky.
Aby sme zistili počet kociek, ktoré sa do boxu zmestia, stačí vypočítať objem boxu – kvádra, ale nie v cm³, ale v kockách 😀
a = 7
b = 4
c = 4
V = ?
V = a ⋅ b ⋅ c
V = 7 ⋅ 4 ⋅ 4
V = 112
Odpoveď: 112
4. príklad
Zadanie:
Lenka ušetrila v januári 22 eur, vo februári 16 eur a v marci 21 eur. Koľko eur ušetrila v apríli, ak za tieto štyri mesiace ušetrila priemerne 20 eur mesačne?
Riešenie:
Priemernú hodnotu vypočítame ako „súčet hodnôt / počet hodnôt“.
V našom prípade:
priemerná hodnota = 20 € = (22 € + 16 € + 21 € + x €) / 4
20 = (59 + x)/4 /⋅4
80 = 59 + x /-59
x = 21 €
Odpoveď: 21
5. príklad
Zadanie:
Pozemok má pôdorys v tvare kosodĺžnika. Na pláne s mierkou 1 : 5 000 má jedna zo strán kosodĺžnika dĺžku 9 cm a priľahlá výška má 7 cm. Koľko hektárov zaberá pozemok v skutočnosti? Výsledok uveď s presnosťou na stotiny.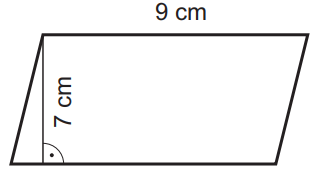
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 15,75
6. príklad
Zadanie:
Marta sa oblieka do školy. Chce si obliecť sukňu, tričko a obuť tenisky. V skrini má 3 sukne rôznej dĺžky, 5 tričiek rôznej farby a 4 páry tenisiek z rôzneho materiálu. Koľkými rôznymi spôsobmi sa Marta môže obliecť a obuť?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 60
7. príklad
Zadanie:
Vypočítaj v stupňoch veľkosť ostrého uhla, ktorý zvierajú ručičky hodín o pol šiestej.
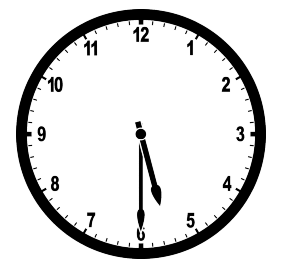
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 15
Zadanie Knižnica
Pán Martin má v knižnici spolu 150 kníh. Roztriedil ich do piatich kategórií. Románov je 75, encyklopédií je 5-krát menej ako románov. Detských kníh má o 4 viac ako cestopisov. V kategórii „hobby“ si nechal 20 kníh.
Na zadanie Knižnica sa vzťahujú úlohy 8 a 9.
8. príklad
Zadanie:
Koľko cestopisov má pán Martin vo svojej knižnici?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 18
9. príklad
Zadanie:
Do jednej z kníh v kategórii „hobby“ si pán Martin odložil úspory. Jeho suseda zaujali práve knihy z tejto kategórie a chcel si nejakú z nich požičať. Aká je pravdepodobnosť, že si náhodou vyberie tú knihu, v ktorej mal pán Martin odložené úspory? Výsledok uveď zlomkom v základnom tvare.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 1/20
10. príklad
Zadanie:
Číselná os na obrázku je rozdelená na 8 zhodných úsekov. Bod A je obrazom reálneho čísla. Uveď toto číslo zlomkom v základnom tvare.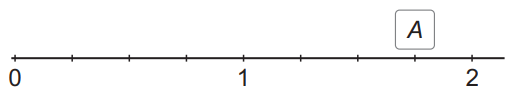
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 7/4
11. príklad
Zadanie:
Vypočítaj
1,5² + 1,6² + 1,7² =
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 7,7
12. príklad
Zadanie:
Mesačník o zdravej výžive bežne stojí 2,90 €. Pán Milan si objednal ročné predplatné, zaplatil zaň 29,50 €. Koľko eur ušetril kúpou predplatného?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 5,30
13. príklad
Zadanie:
Osemuholník ABCDEFGH sa skladá z ôsmich zhodných trojuholníkov. Obsah tohto osemuholníka je 33,6 cm². Vypočítaj obsah časti vyfarbenej tmavou farbou. Výsledok uveď v cm².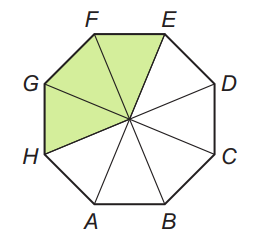
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 12,6
Zadanie Pracovný stôl
Pracovná doska stola má byť umiestnená v rohu kancelárie. Jej podstava má tvar štvrťkruhu, pričom polomer kruhu je 90 cm. Hrúbka dosky je 2 cm.
Na zadanie Pracovný stôl sa vzťahujú úlohy 14 a 15
14. príklad
Zadanie:
Hrany pracovnej dosky sa upravia tak, že sa po celom obvode dosky nažehlí hranovacia páska. Koľko centimetrov hranovacej pásky sa spotrebuje na olemovanie jednej pracovnej dosky? Počítaj s hodnotou π = 3,14. Výsledok zaokrúhli na celé centimetre nahor.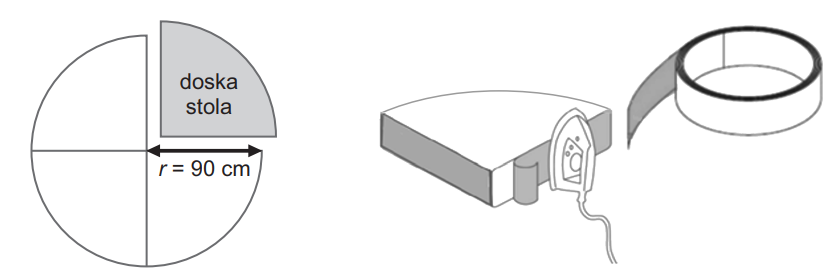
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 322
15. príklad
Zadanie:
Pracovné dosky sa vyrezávajú z dosiek s podstavou v tvare štvorca so stranou dĺžky 180 cm. Koľko percent tvorí odpad pri vyrezaní štyroch takýchto pracovných dosiek? Počítaj s hodnotou π = 3,14.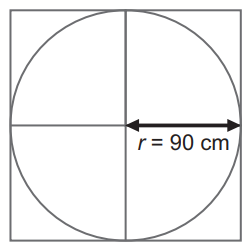
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: 21,5
16. príklad
Zadanie:
Pani Klára má vo svojej banke povolené prečerpanie účtu. Aktuálne je na jej účte mínusový zostatok –125,80 €. Po pripísaní výplaty sa suma na jej účte zmenila na 721,50 €. Vypočítaj výšku výplaty pani Kláry v eurách.
A: 595,70
B: 606,70
C: 846,30
D: 847,30
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
17. príklad
Zadanie:
Priamka k je rovnobežná s priamkou l. Priamka m je kolmá na priamku k. Priesečník priamok k a m označme A. Priesečník priamok l a m označme B. Priamka n je rôznobežná so všetkými predchádzajúcimi priamkami a priesečník priamok m a n neleží na úsečke AB. Priesečník priamok l a n označme C. Priesečník priamok k a n označme D. Na základe toho, čo vieme o vzájomnej polohe uvedených priamok, je štvoruholník ABCD
určite
A: obdĺžnik.
B: lichobežník.
C: kosodĺžnik.
D: štvorec.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
18. príklad
Zadanie:
Na obrázku sú 3 telesá. Hrana kocky je dlhá 3 cm. Kváder má dva rozmery rovnaké ako kocka, jeho tretí rozmer je 2-krát dlhší. Valec je rovnako vysoký ako kocka a priemer jeho podstavy je 3 cm.
Z týchto troch telies možno postaviť rôzne stavby. Predpokladajme, že kváder v stavbe je položený ako na obrázku. V nasledujúcich možnostiach sú uvedené pohľady zhora na niektoré z týchto stavieb. V ktorej možnosti je pohľad na stavbu z týchto troch telies, ktorá by určite nemohla mať práve dve poschodia?
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
Zadanie Heslo
Otec nechal synovi nasledujúci odkaz: „Ak chceš vedieť heslo na wifi, usporiadaj čísla od najmenšieho po najväčšie.“
Na zadanie Heslo sa vzťahujú úlohy 19 a 20.
19. príklad
Zadanie:
Ktoré heslo na wifi je správne?
A: LPMS B: MSPL C: PSLM D: SMPL
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
20. príklad
Zadanie:
Predpokladajme, že sa synovi nechcelo zoraďovať čísla do správneho poradia. Aká je pravdepodobnosť, že náhodne zadá správne heslo na prvý pokus? Výsledok zaokrúhli na desatiny.
A: 4,2%
B: 5,6%
C: 8,3%
D: 16,7%
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: A
21. príklad
Zadanie:
Jolana číta detektívku. Prečítala už 270 strán. Koľko strán má celá detektívka, ak Jolane do konca ostáva prečítať ešte dve pätiny knihy?
A: 162
B: 180
C: 450
D: 675
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
22. príklad
Zadanie:
Vypočítaj hodnotu y pre x = –2 podľa nasledujúcej schémy.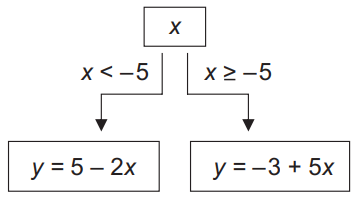
A: 9 B: -4 C: -6 D: -13
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: D
23. príklad
Zadanie:
Štyria súrodenci si sporia na spoločnú elektrickú kolobežku. Tomáš nasporil o 30 € viac než Eva, Roman 2-krát viac ako Eva a Soňa o 20 % viac ako Eva. Spolu už nasporili 290 €. Ktoré z nasledujúcich tvrdení je nesprávne?
A: Sestry nasporili menej ako ich bratia.
B: Bratia spolu nasporili 3-krát viac ako Soňa.
C: Tomáš nasporil o 20 € viac ako Roman.
D: Eva nasporila o 10 € menej ako Soňa.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
24. príklad
Zadanie:
Na číselnej osi je vyznačený obraz čísla a.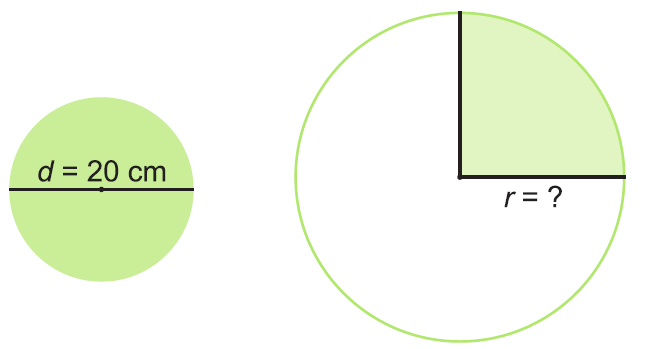
A: Ani jeden vzťah neplatí.
B: Platí 2., 4. a 5. vzťah.
C: Platí iba 1. a 3. vzťah.
Platí iba 2. a 4. vzťah.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
25. príklad
Zadanie:
V štvorcovej sieti so stranou štvorca dlhou 1 cm sú znázornené 4 štvoruholníky, medzi ktorými je aj pravouhlý lichobežník. V ktorej možnosti je správne uvedený jeho obsah?
A: 18 cm² B: 17,5 cm² C: 15 cm² D: 13,5 cm²
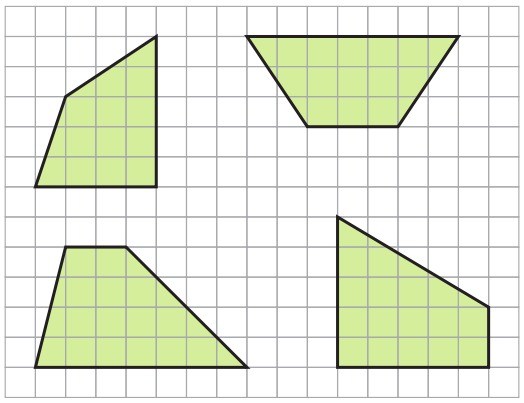
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
Zadanie Slovenské jaskyne
Správa slovenských jaskýň má na starosti ochranu a prevádzku trinástich sprístupnených jaskýň. Päť z nich je zároveň zapísaných do Zoznamu svetového kultúrneho a prírodného dedičstva UNESCO. V grafe je znázornený prehľad návštevnosti piatich vybraných jaskýň v rokoch 2016 – 2018.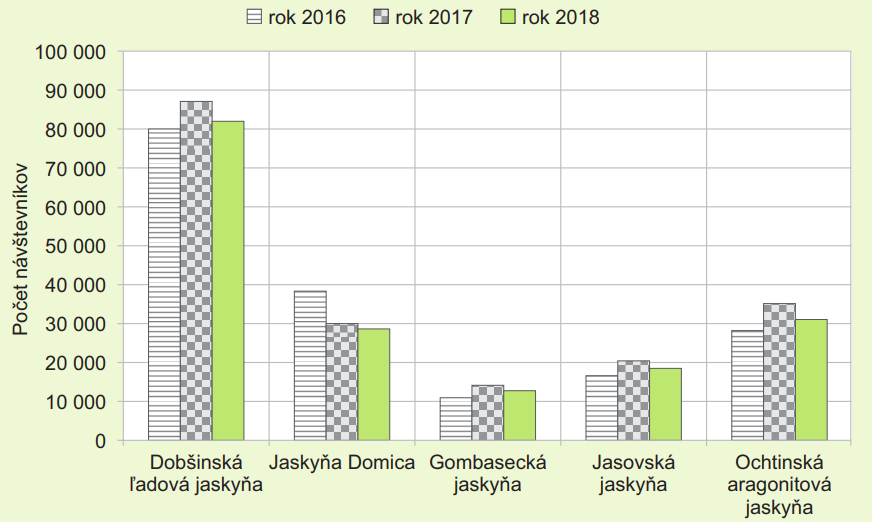
V tabuľke sú uvedené základné údaje z roku 2018 týkajúce sa týchto jaskýň.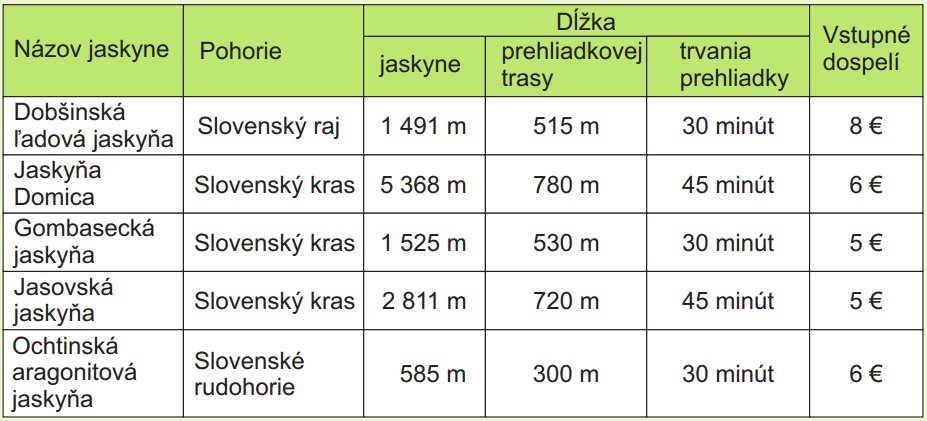
Na zadanie Slovenské jaskyne sa vzťahujú úlohy 26 a 27.
26. príklad
Zadanie:
Rozhodni o pravdivosti nasledujúcich dvoch tvrdení:
1. Len v jednej z vybraných jaskýň bola návštevnosť v roku 2018 nižšia ako v roku 2016.
2. Ochtinskú aragonitovú jaskyňu navštívilo počas sledovaného obdobia viac ako 120-tisíc návštevníkov.
A: Iba prvé tvrdenie je pravdivé.
B: Iba druhé tvrdenie je pravdivé.
C: Pravdivé sú obe tvrdenia.
D: Pravdivé nie je ani jedno tvrdenie.
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: A
27. príklad
Zadanie:
V ktorej z vybraných jaskýň návštevník nebol, ak počas prehliadok ostatných štyroch jaskýň nachodil spolu 2 315 m a na vstupnom zaplatil spolu 25 €?
A: Dobšinská ľadová jaskyňa
B: Jaskyňa Domica
C: Gombasecká jaskyňa
D: Jasovská jaskyňa
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
Zadanie Vyvýšený zákon
Vyvýšený záhon má tvar kvádra. Jeho dno má rozmery 1,5 m a 90 cm. Výplň záhona tvoria 4 vrstvy tak, ako je znázornené na obrázku.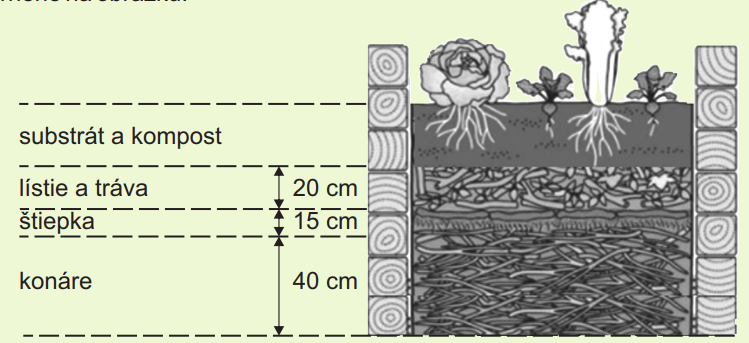
Na zadanie Vyvýšený zákon sa vzťahujú úlohy 28 a 29.
28. príklad
Zadanie:
Koľko centimetrov má výška vrstvy tvorenej substrátom a kompostom, ak pomer výšky tejto vrstvy a výšky vrstvy konárov je 5 : 8?
A: 40
B: 25
C: 46
D: 29
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: B
29. príklad
Zadanie:
V ktorej možnosti je správne uvedený objem vrstvy konárov vo vyvýšenom záhone?
A: 54 dm³ B: 5,4 m³ C: 540 l D: 0,54 hl
Riešenie: Získať prístup k riešeniu príkladov
Odpoveď: C
30. príklad
Zadanie:
Vypočítaj obsah pravouhlého trojuholníka ABC, ak poznáš obsah štvorca nad preponou BC a tiež obsah štvorca nad odvesnou AC.
A: 54 cm² B: 36 cm² C: 108 cm² D: 135 cm²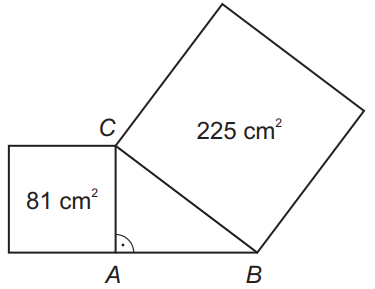
Riešenie: Získať prístup k riešeniu príkladov
