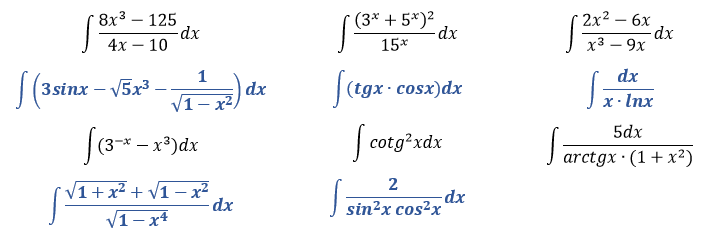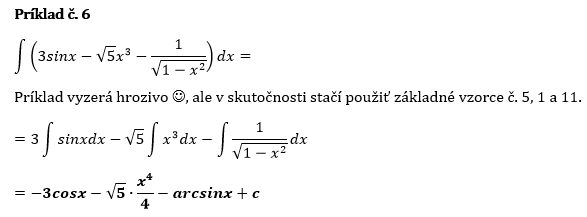Pri výpočte nasledovných neurčitých integrálov budeme využívať iba základné vzorce na integrovanie, ktoré nájdete v článku Základné integračné vzorce a pravidlá.
Príklad č. 1
![]()
Integrál rozdelíme na 3, pričom čísla 3 a 5 vyjmeme pred čiastkové integrály.
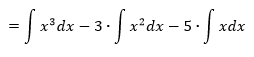
Následne využijeme základný vzorec č. 1.

Upravíme na zlomky v základnom tvare.
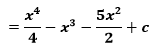
Príklad č. 2
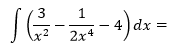
Integrál rozdelíme na 3, pričom prvé dva zlomky upravíme na mocniny so záporným mocniteľom a čísla 3 a 1/2 vyjmeme pred integrály.
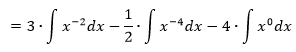
Opäť využijeme základný vzorec č. 1.
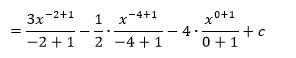
A zjednodušíme.
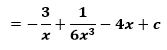
Príklad č. 3
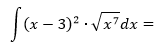
Najskôr umocníme dvojčlen a odmocninu upravíme na mocninu s racionálnym mocniteľom.
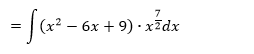
3-člen v zátvorke vynásobíme mocninou . Využijeme vzorec
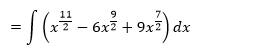
Rozdelíme na 3 integrály, z 2. a 3. integrálu vyjmeme čísla 6 a 9 a integrujeme podľa vzorca č. 1.
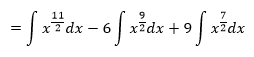
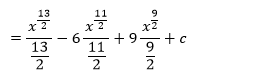
a upravíme
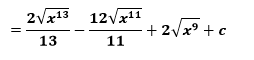
Príklad č. 4
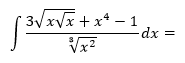
Najskôr „odstránime“ odmocniny, teda upravíme ich na mocniny s racionálnym mocniteľom a v prípade potreby vynásobíme.

Rozdelíme na 3 integrály, z 1. integrálu vyjmeme číslo 3 a integrujeme podľa vzorca č. 1.
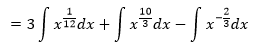

A následne už len zlomky zjednodušíme.
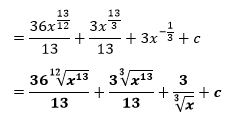
Pre členov Pohodovej matematiky sú pripravené aj riešenia nasledovných integrálov: