V článku Kvadratická funkcia a jej graf sme sa naučili jednoduchý spôsob, ako načrtnúť graf kvadratickej funkcie. Stačilo nám zistiť súradnice vrcholu, priesečník s osou y a vedieť, či koeficient a je číslo záporné alebo kladné.
Ak niektorí z vás pri svojich pokusoch používali aj náš Kreslič kvadratických funkcií, tak ste si určite všimli, že raz je graf posunutý vľavo, raz vpravo, raz je vyššie, inokedy nižšie, niekedy je štíhly a niekedy zase široký.
Čo spôsobuje zmenu tvaru paraboly?
Viacerí asi už z názvu tohto článku pochopili, že príčinou budú pravdepodobne koeficienty a, b, c v predpise kvadratickej funkcie.
Poďme sa teda spolu pozrieť, aké zmeny spôsobuje zmena koeficientu a.
Daných je 5 kvadratických funkcií:
f: y = x2
g: y = 2x2
h: y = 3x2
i: y = 0,5x2
j: y = 0,3x2
Určte súradnice vrcholov v prípade všetkých funkcií.
Určite ste zistili, že vo všetkých prípadoch
V = [0; 0]
Súradnice vrcholu sa v tomto prípade nezmenili. Čo sa teda zmenilo?
Doplňte si nasledovnú tabuľku funkčných hodnôt (v zošite) a na základe nej načrtnite do jednej súradnicovej sústavy grafy daných 5 funkcií.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f(x) | |||||
| g(x) | |||||
| h(x) | |||||
| i(x) | |||||
| j(x) |
Vaše náčrty budú vyzerať približne takto:

Čo ste zistili?
Oproti grafu základnej kvadratickej funkcie y = x2, kde a=1:
- keď sa hodnota a blíži od 1 k 0, tak parabola je stále „tlstejšia a tlstejšia“
- naopak, keď je hodnota a väčšia ako 1 a stále vzrastá, tak parabola sa stáva „štíhlejšou“
A aké zmeny spôsobuje zmena koeficientu c?
Teraz stačí ak využijeme iba 3 funkcie a zmena bude badateľná veľmi rýchlo.
Sú dané 3 kvadratické funkcie:
f: y = x2
g: y = x2 + 2
h: y = x2 – 3
Doplňte si nasledovnú tabuľku funkčných hodnôt a načrtnite do jednej súradnicovej sústavy grafy daných 3 funkcií.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f(x) | |||||
| g(x) | |||||
| h(x) |
Vaše náčrty budú vyzerať približne takto:
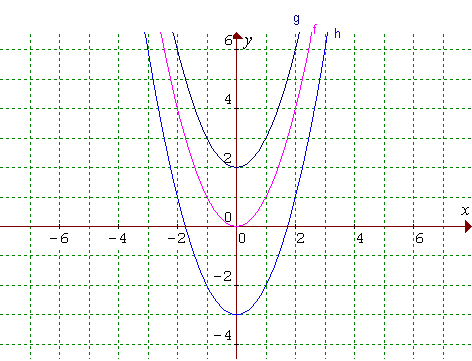
Čo ste zistili?
Oproti grafu základnej kvadratickej funkcie y = x2, kde a=1:
- keď sa hodnota c zväčšuje, tak parabola sa posúva nahor v smere osi y
- naopak, keď sa hodnota c zmenšuje, tak parabola sa posúva nadol v smere osi y
Je samozrejmé, že podobne by to platilo i v prípadoch funkcií y = (x-3)2, y = 2(x-3)2, y = 5(x-3)2, y = 0,7(x-3)2, …, y = -(x-3)2, y = -2(x-3)2, y = -5(x-3)2, y = -0,7(x-3)2, … alebo pri zmene koeficientu c napr. v prípade funkcií y = (x-3)2 – 3, y = -2(x-3)2 – 5, y = 5(x-3)2 + 5, y = -0,7(x-3)2 + 1, …
A čo v prípade zmeny koeficientu b?
Posúďte sami:
f: y = x2 – 2x + 1
g: y = x2 – 6x + 1
h: y = x2 + 4x + 1
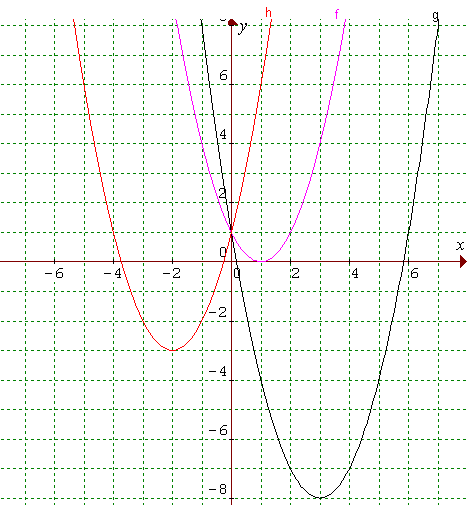
Všimli ste si, že zmena samotného koeficientu b posúva graf tak v smere osi y ako aj v smere osi x? Čím to bude?
Ľahká otázka, keď viete, že vrchol paraboly je bod [-b/2a;f(-b/2a)]. Čiže pri zmene b sa mení x-ová aj y-ová súradnica vrcholu paraboly.
Často sa stáva, že kvadratickú funkciu máte zapísanú napr. v tvare y = -2·(x-1)2 + 3.
Posunutie základného grafu bude:
- zistíme, pre akú hodnotu x je výraz v zátvorke rovný 0 … x-1=0 pre x=1, teda graf posunieme o 1 doprava
- pozrieme na číslo za mocninou … +3 … čiže parabola sa ešte posunie o 3 nahor
Pravdepodobne ste si uvedomili, že hodnoty 1 a 3 sú vlastne súradnice vrcholu paraboly.
