Obsah článku:
Číslica:
je grafický znak, pomocou ktorého zapisujeme číslo a vyjadrujeme množstvo. Napr. v desiatkovej sústave sa používajú arabské číslice, znaky, ktoré predstavujú čísla od jedna do deväť.
Číslo:
Pojem čísla sa v histórii postupne rozširoval a podobne je to aj v matematike, kde sa postupne zoznamujeme s týmito druhmi čísel:
- Prirodzené čísla 1, 2, 3, … slúžia k vyjadreniu počtu prvkov konečných neprázdnych množín alebo poradia prvkov v usporiadaných skupinách.
- Nula – „0“ slúži na vyjadrenie počtu prvkov prázdnej množiny. V niektorých prípadoch sa zaraďuje nula medzi prirodzené čísla
- Celé čísla …, -2, -1, 0, 1, 2, … sú všetky prirodzené čísla doplnené o nulu a čísla k nim opačné. Umožňujú vyjadriť zmeny počtu prvkov a ich porovnávanie, prírastok, úbytok
- Racionálne čísla sú čísla, ktoré je možné zapísať v tvare zlomku a/b, kde p je celé číslo a q je prirodzené číslo. Používajú sa k vyjadreniu počtu celkov a ich častí, zmien týchto počtov a pod.
- Reálne čísla sú všetky čísla racionálne a čísla iracionálne napr.
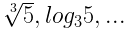
- Komplexné čísla sú všetky reálne čísla a imaginárne čísla (3i, 7 – 2i, …).
Konštanta
je symbol, ktorý označuje určitý objekt z danej množiny objektov. Napr. 4 (označuje číslo 4), π (označuje Ludolfovo číslo).
Premenná
je symbol, ktorý označuje ktorýkoľvek objekt z danej množiny objektov. Spravidla je to písmeno x, y, z …
Množina konštánt, ktoré zastupuje premenná sa nazýva obor premennej.
Prvky oboru premennej sa nazývajú hodnoty premennej.
Dosadenie konštanty za premennú
Nahradenie premennej konštantou z oboru premennej v nejakom výraze nazývame dosadenie konštanty za premennú do daného výrazu.
Príklad 1:
Zapíšte pomocou premenných súčet druhých mocnín dvoch za sebou idúcich párnych prirodzených čísel.
Riešenie:
a) Klikaním na tlačidlo ďalej sa bude vykresľovať riešenie príkladu:
Príklad 2:
Rozhodnite, ktoré znaky vo výrazoch sú premennými a ktoré konštantami:
a) 4x2–y2; x,y∈R
b) S = πr2 (obsah kruhu)
Riešenie:
a) konštanty: 4; premenné: x,y; obor oboch premenných je množina R
b) konštanta: π; premenné: S, r; obor premenných je množina R+
Matematizácia slovnej úlohy
je matematické vyjadrenie textu slovnej úlohy, ktorá predstavuje fyzikálny, technický alebo iný problém.
Postup je zvyčajne nasledovný:
- Vytvoríme matematický model danej úlohy, ktorým je najčastejšie aritmetická alebo algebraická úloha vyjadrená rovnicami resp. nerovnicami.
- Vyriešime matematickú úlohu: aritmetickú úlohu riešime úsudkom, algebraickú riešením rovníc resp. nerovníc.
- Získané výsledky prevedieme do reálnej situácie alebo vyberiem také riešenia matematickej úlohy, ktoré sú riešeniami daného problému.
Príklad 3:
V triede je 30 žiakov. Z písomnej práce malo menej ako 20 bodov práve 70% žiakov a to 87,5% všetkých chlapcov a 50% všetkých dievčat. Koľko chlapcov a dievčat je v triede?
Riešenie:
Zvolíme si neznámu: napr. nech je v triede x dievčat. Obor premennej x je množinavšetkých kladných celých čísel
počet dievčat ……….. x
počet chlapcov …….. 30–x
Celkový počet žiakov, ktorí mali menej ako 20 bodov je 70% z 30 žiakov, teda
0,7.30=21.
Z toho chlapcov je 87,5% z počtu všetkých chlapcov, teda
0,875.(30–x)=26,25–0,875x
a dievčat je 50% z počtu všetkých dievčat, teda
0,5x .
Získali sme rovnicu:
(26,25–0,875x)+0,5x=21
Po vyriešení
x=14
spĺňa podmienky riešiteľnosti, preto:
počet dievčat …….. 14
počet chlapcov ….. 30–14=16
Odpoveď:
V triede je 14 dievčat a 16 chlapcov.
