Výrokové formy, kvantifikované výroky

Neriešené príklady

Príklad 1:

Ktoré z daných slovných výrazov predstavujú výrokové formy.

1. 2x – 3y ≤ 5; x, y ∈ R.
2. Človek a je otcom človeka b (a, b ∈ U).
3. Číslo x je deliteľné číslom 7 (x ∈ N).
4. Obsah obdĺžnika s dĺžkami strán x, y je väčší ako obsah štvorca so stranou x (x, y ∈ R₊).
5. Obvod obdĺžnika s dĺžkami strán x, y a obvod štvorca so stranou x (x, y ∈ R₊).
6. Otec súrodencov a, b (a, b ∈ U)
7. Dĺžka uhlopriečky štvorca so stranou a je číslo deliteľné štyrmi (a ∈ R₊)

---

Príklad 2:

Znázornite graficky na číselnej osi údaje o počte objektov „nikto“, „aspoň jeden“, „najviac jeden“, „aspoň dva“, „najviac dva“, „práve dva“, „najmenej päť“, „najviac 7“.

---

Príklad 3:

Znázornite na číselnej osi údaje o počte prvkov množín, ktoré sú vyjadrené pomocou kvantifikátorov nasledovne:

a) V našej triede nikto nenosí okuliare.
b) Najviac jeden spolužiak sa zúčastní matematickej súťaže MAKS.
c) Aspoň traja chlapci našej školy budú reprezentovať na majstrovstvách Slovenska v šachu.
d)Práve štyria žiaci sa nezúčastnili výchovného koncertu v Dome odborov.
e) Aspoň jeden z nás sa bude pozerať večer na Televízne noviny.
f) Najviac traja môžu postúpiť do krajského kola Olympiády v ruskom jazyku.

---

Príklad 4:

Zapíšte symbolicky pomocou premenných a kvantifikátorov (∀, ∃) tieto všeobecné a existenčné výroky:

a) Existuje reálne číslo, ktorého druhá mocnina je rovná 4.
b) Pre každé prirodzené číslo platí, že jeho tretia mocnina je párne číslo.
c) Existuje celé číslo, z ktorého druhá odmocnina je 2.
d) Pre každé celé číslo platí, že jeho absolútna hodnota je väčšia alebo rovná 0.

---

Príklad 5:

V nasledujúcich výrokoch nahraďte kvantifikátory existenčným alebo všeobecným kvantifikátorom:

a) Niektorí žiaci 1. C majú domácu úlohu.
b) Ľubovoľné číslo je prirodzené.
c) Niektorý trojuholník je pravouhlý.
d) Absolútna hodnota ľubovoľného reálneho čísla je nezáporné reálne číslo.
e) Nikto z 1. A nevyriešil danú úlohu správne.
f) Ľubovoľné prirodzené číslo deliteľné číslom 6 je zloženým číslom.

---

Riešenie príkladov č. 1 a 2:

1. príklad: výrokovými formami sú všetky slovné výrazy okrem e), f)

2. príklad: grafické znázornenie:

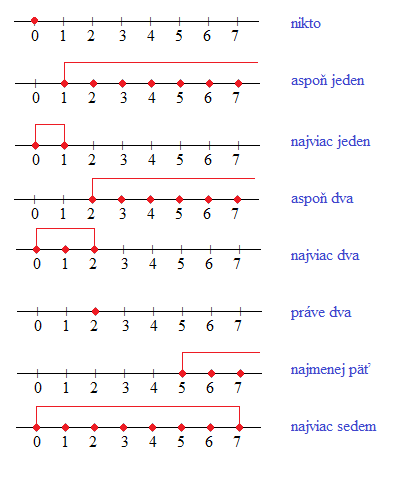
3. príklad: grafické znázornenie:

4. príklad:
a) ∃x∈R; x²=4;
b) ∀x∈N; 2|x³;
c) ∃x∈Z; √x = 2;
d) ∀x∈Z; |x|≥0;

5. príklad:
Existujú žiaci 1. C, ktorí majú domácu úlohu.
Každé číslo je prirodzené.
Existuje trojuholník, ktorý je pravouhlý.
Pre všetky reálne čísla platí, že ich absolútna hodnota je nezáporné reálne číslo.
Každý žiak z 1. A vyriešil danú úlohu nesprávne.
Každé prirodzené číslo deliteľné číslom 6 je zloženým číslom.