Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
1. príklad
Zadanie:
Alica si kúpila zmes orechov obsahujúcu kešu orechy, lieskové orechy a arašidy zastúpené v pomere 1:2:3. Vypočítajte v gramoch hmotnosť celej zmesi, ak arašidy majú hmotnosť 90 g.
Riešenie:
kešu orechy, lieskové orechy a arašidy ………… 1:2:3
hmotnosť arašidov …. 90 g
počet dielov arašidov …. 3
1 diel …. 90 : 3 = 30 g
počet dielov kešu ….. 1
hmotnosť kešu ….. 30 g
počet dielov lieskových orechov ….. 2
hmotnosť lieskových orechov ….. 2 . 30 = 60 g
spolu …………… 90 + 30 + 60 = 180 g
Hmotnosť celej zmesi bola 180 g.
2. príklad
Zadanie:
Na obrázku je stavba z kociek, pričom susedné kocky sa dotýkajú celými stenami a nie sú zlepené. Dvadsať žiakov malo odpovedať na otázku, z koľkých kociek je postavená táto stavba. Ich odpovede sú znázornené pomocou kruhového diagramu. Koľko percent žiakov odpovedalo správne?
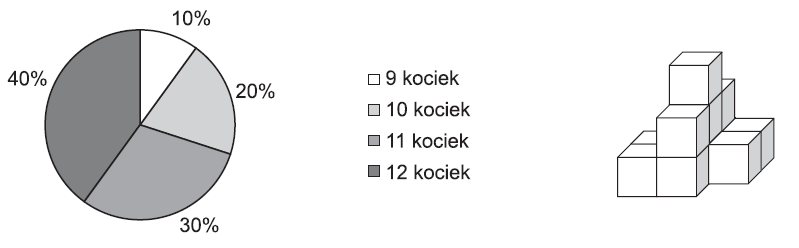
Riešenie:
Najskôr zistíme, koľko kociek je na obrázku.
- keďže kocky nie sú zlepené, tak aby 3 kocky v strede na 2. podlaží nespadli, musia byť kocky aj pod nimi , preto 3+3=6
- úplne hore je 1 kocka
- vpravo sú 2 kocky
- vľavo sú 2 kocky
- spolu … 6 + 1 + 2 + 2 = 11 kociek
Odpoveď 11 kociek zvolilo 30% žiakov.
3. príklad
Zadanie:
Na farme spolu chovajú 110 kusov hydiny (sliepky, morky, kačky a husi). Sliepky predstavujú polovicu, moriek je 10 a kačiek je o 7 viac ako husí. Koľko husí chovajú na farme?
Riešenie:
spolu ……. 110
sliepky ….. polovica ….. 110:2=55
morky ….. 10
husi ………. x
kačky ……. x+7
110 = 55 + 10 + x + x+7
110 = 72 + 2x / -72
38 = 2x / :2
19 = x
Na farme chovajú 19 husí.
4. príklad
Zadanie:
Koľkokrát je číslo 5 . 105 väčšie ako číslo 125 . 103?
Riešenie:
5 . 105 = 5 . 10 . 10 .103 = 5 . 5.2 . 5.2 .103 =
= 5 . 5 . 5 . 2 . 2 . 103= 4 . 125 . 103
Číslo 5 . 105 je 4-krát väčšie ako číslo 125 . 103.
5. príklad
Zadanie:
Riešte nerovnicu 2x-77>93 a určte, koľko dvojciferných čísel je riešením tejto nerovnice.
Riešenie:
2x – 77 > 93 /+77
2x > 170 / : 2
x > 85
Riešením sú dvojciferné čísla od 86 do 99 … 14 čísel
Riešením nerovnice je 14 dvojciferných čísel.
6. príklad
Zadanie:
Zo štvorca ABCD so stranou dĺžky 12,7 cm sme vystrihli štvorec KLMN so stranou dĺžky 5,8 cm, ako je znázornené na obrázku. Vypočítajte v cm obvod osemuholníka ABCMLKND.
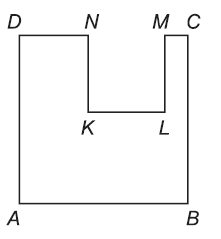
Riešenie:
Obvod je tvorený 3 stranami veľkého štvorca … |DA| + |AB| + |BC| = 12,7 + 12,7 + 12,7 = 38,1 cm
Ďalej sú súčasťou obvodu úsečky DN, KL a MC, pre ktoré platí:
|DN| + |KL| + |MC| = |AB| = 12,7 cm
A nakoniec sú súčasťou obvodu ešte 2 strany malého štvorca …. |NK| + |LM| = 5,8 + 5,8 = 11,6 cm
Obvod = 38,1 + 12,7 + 11,6 = 62,4 cm
Obvod osemuholníka ABCMLKND je 62,4 cm.
7. príklad
Zadanie:
Jano, Alena a Karol spolu nazbierali 40% hmotnosti papiera z celej triedy. Jano nazbieral 93 kg, Alena nazbierala 81 kg a Karol nazbieral 96 kg. Koľko kg papiera nazbierali všetci žiaci tejto triedy?
Riešenie:
Jano + Alena + Karol = 93 + 81 + 96 = 270 kg ……. 40%
1% = 270 : 40 = 6,75
všetci žiaci …. 100% ….. 100 . 6,75 = 675 kg
Všetci žiaci nazbierali 675 kg papiera.
8. príklad
Zadanie:
Počas automatického ladenia TV prijímač vyhľadal 25 kanálov, z toho boli 4 hudobné. Kanály sa do pamäte TV prijímača ukladajú v náhodnom poradí. Vyjadrite v percentách pravdepodobnosť udalosti, že ako prvý bude uložený hudobný kanál.
Riešenie:
Počet priaznivých možností … 4
Počet všetkých možností …….. 25
Pravdepodobnosť = počet priaz. mož. : počet všetkých mož.
P(A) = 4 : 25 = 0,16 = 16%
Hudobný kanál bude uložený ako prvý s pravdepodobnosťou 16%.
9. príklad
Zadanie:
Vypočítajte dve tretiny z troch štvrtín. Výsledok zapíšte zlomkom v základnom tvare.
Riešenie:
2/3 z 3/4 = 2/3 * 3/4 = (2.3) / (3.4)
… čitateľ aj menovateľ vydelíme číslom 3
2/4
…. čitateľ aj menovateľ vydelíme číslom 2
1/2
10. príklad
Zadanie:
Traja súrodenci si objednali jednu pizzu veľkosti XL. Miška zjedla štvrtinu z celej pizze. Lenka zjedla tretinu zvyšku a Patrik zjedol polovicu z toho, čo nechala Lenka. Zvyšok si dali zabaliť domov. Akú časť pizze im zabalili? Výsledok zapíšte zlomkom v základnom tvare.
Riešenie:
Miška …. 1/4
Lenka … 1/3 zo zvyšku … 1/3 . (1-1/4) = 1/3 . 3/4 = 3/12 = 1/4
Miška a Lenka zjedli spolu 1/4 + 1/4 = 2/4 = 1/2
Ešte zostala 1/2, z ktorej zjedol Patrik polovicu, teda 1/2 . 1/2 = 1/4
Takže Miška + Lenka + Patrik = 1/4 + 1/4 + 1/4 = 3/4
Zostalo … 1 – 3/4 = 4/4 – 3/4 = 1/4
Domov im zabalili 1/4 pizze.
11. príklad
Zadanie:
Anna si pripravuje na raňajky ovsenú, pohánkovú alebo pšenovú kašu s jedným z troch druhov ovocia, ochutenú medom alebo kakaom. Koľko rôznych druhov raňajok si môže pripraviť z uvedených surovín?
| Kaša | Ovocie | Na dochutenie |
|---|---|---|
| ovsená, pohánková, pšenová | jablká, hrušky, slivky | med, kakao |
Riešenie:
S každým druhom kaše si môže skombinovať 3 druhy ovocia a k tomu si dať med alebo kakao. Jeden zo spôsobov riešenia teda môže byť súčin: 3 . 3 . 2 = 18
Alebo môžeme vypisovaním:
OJM, OJK, OHM, OHK, OSM, OSK,
PJM, PJK, PHM, PHK, PSM, PSK,
PšJM, PšJK, PšHM, PšHK, PšSM, PšSK
teda 18 možností
Z uvedených druhov surovín si môže pripraviť 18 druhov raňajok.
12. príklad
Zadanie:
Paulína má stovky svojich fotografií z dovolenky uložené na pamäťových kartách. Všetky fotografie dala vytlačiť. V tabuľke sú uvedené počty fotografií a ceny za ich vytlačenie. Koľko eur zaplatila Paulína za vytlačenie všetkých fotografií s rozmermi 10cm x 15cm?
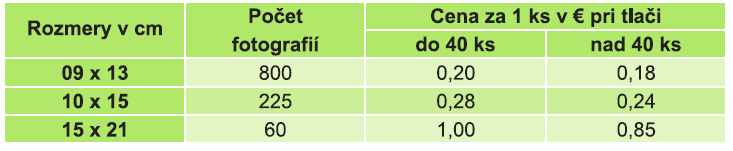
Riešenie:
Počet fotografií s rozmermi 10 x 15 ….. 225
225 fotografií je viac ako 40, preto
cena za 1 ks ….. 0,24 €
225 fotografií ……. 225 . 0,24 = 54 €
Paulína zaplatila za vytlačenie fotografií s rozmermi 10cm x 15cm 54 eur.
13. príklad
Zadanie:
Škatuľka v tvare kvádra má rozmery 12 cm, 8 cm a 5 cm. Vypočítajte jej objem v litroch. Výsledok uveďte s presnosťou na dve desatinné miesta.
Riešenie:
Objem kvádra …. V = a . b . c
a = 12 cm
b = 8 cm
c = 5 cm
V = ? l .
V = a . b . c
V = 12 . 8 . 5
V = 480 cm3 = 0,48 dm3 = 0,48 l
Objem škatuľky je 0,48 l.
14. príklad
Zadanie:
Za domom stojí sud, v ktorom je 0,25 m3 dažďovej vody. Starý otec z neho postupne vyberá 12-litrovou krhlou vodu na polievanie, až kým pri dne neostane posledných 10 litrov vody. Najviac koľko plných krhiel mohol z tohto suda starý otec naplniť?
Riešenie:
objem vody v sude …. 0,25 m3 = 250 dm3 = 250 l
zostalo na dne …… 10 l
objem vody vybranej v krhlách …… 250 – 10 = 240 l
objem 1 krhly …… 12 l
počet krhiel = 240 : 12 = 20
Starý otec mohol naplniť najviac 20 plných krhiel.
15. príklad
Zadanie:
Súrodenci Novákovci potrebovali odvážiť psov Bima a Astu. Psy odmietali pokojne sedieť na váhe, preto sa odvážili spolu s nimi tak, ako je znázornené na obrázkoch. Koľko kilogramov vážila Asta?
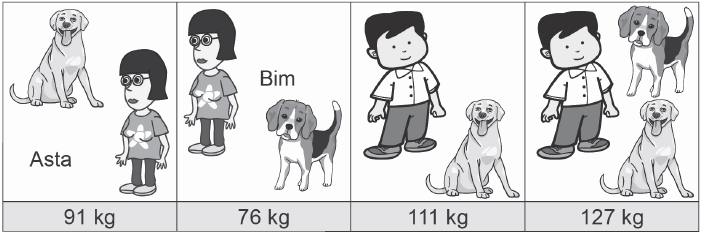
Riešenie:
dievča + Asta = 91 kg
dievča + Bim = 76 kg
chlapec + Asta = 111 kg
chlapec + Asta + Bim = 127 kg
Keďže poznáme celkovú hmotnosť chlapca a Asty, môžeme tento údaj dosadiť do poslednej rovnice a vypočítať tak hmotnosť Bima.
chlapec + Asta + Bim = 127 kg
111 kg + Bim = 127 kg / – 111 kg
Bim = 16 kg
Pomocou vypočítanej hmotnosti Bima určíme z druhej rovnice hmotnosť dievčaťa.
dievča + Bim = 76 kg
dievča + 16 kg = 76 kg / -16 kg
dievča = 60 kg
Pomocou vypočítanej hmotnosti dievčaťa určíme z prvej rovnice hmotnosť Asty.
dievča + Asta = 91 kg
60 kg + Asta = 91 kg / – 60 kg
Asta = 31 kg
Asta vážila 31 kilogramov.
16. príklad
Zadanie:
Pán Novák cvičil na lúke psov Bima a Astu. V istom momente bol od neho Bim vzdialený 24 metrov a Asta 17 metrov. Ktorá z nasledujúcich možností nemohla nastať?
Psy boli od seba vzdialené
A: 6 m
B: 7 m
C: 30 m
D: 41 m
Riešenie:
Pán Novák, Bim a Asta vytvárajú trojuholník alebo sa nachádzajú na priamke.. Ideme teda zisťovať, či je možné z uvedených rozmerov „zostrojiť“ trojuholník.
Musí platiť: Súčet dvoch menších strán je väčší ako tretia strana.
A: 6 m, 17 m, 24 m
6 + 17 = 23 a to nie je menej ako 24, preto nevyhovuje možnosť A.
Pre „istotu“ môžeme overiť aj zostávajúce možnosti.
B: 7 m, 17 m, 24 m
7 + 17 = 24 a to sa rovná tretej strane, teda nachádzajú sa na priamke.
C: 30 m, 17 m, 24 m
17 + 24 = 41 > 30, platí, vytvárajú trojuholník
D: 41 m, 17 m, 24 m
17 + 24 = 41 a to sa rovná tretej strane, teda nachádzajú sa na priamke.
Odpoveď: A
17. príklad
Zadanie:
Vypočítajte hodnotu výrazu 2x + 3 . (2 – y) pre x = 3 a y = -1.
A: 9
B: 13
C: 14
D: 15
Riešenie:
Za x dosadíme 3 a za y dosadíme -1.
2.3 + 3 . (2 – (-1)) =
6 + 3 . (2 + 1) =
6 + 3 . 3 =
6 + 9 =
15
Odpoveď: D
18. príklad
Zadanie:
V prepravke sa nachádza niekoľko melónov. Počet melónov v prepravke označme p a hmotnosť všetkých melónov v prepravke vyjadrenú v kilogramoch označme m. Pomocou ktorého výpočtu zistíme priemernú hmotnosť melónov v prepravke v kilogramoch?
A: m : p
B: m – p
C: p . m
D: p : m
Riešenie:
Priemer vypočítame tak, že súčet všetkých hodnôt vydelíme ich počtom. V našom prípade teda celkovú hmotnosť melónov vydelíme počtom melónov – m : p
Odpoveď: A
19. príklad
Zadanie:
Dana si nakreslila otvorenú izbu v tvare kocky. Keby vošla do takejto izby, uvidela by po ľavej ruke stenu s oknom a po pravej ruke stenu s poličkami. Dana chcela urobiť takúto izbu pre sestrinu bábiku. Nakreslila niekoľko sietí pozostávajúcich z piatich štvorcov. Ktorá zo sietí nie je nakreslená správne?
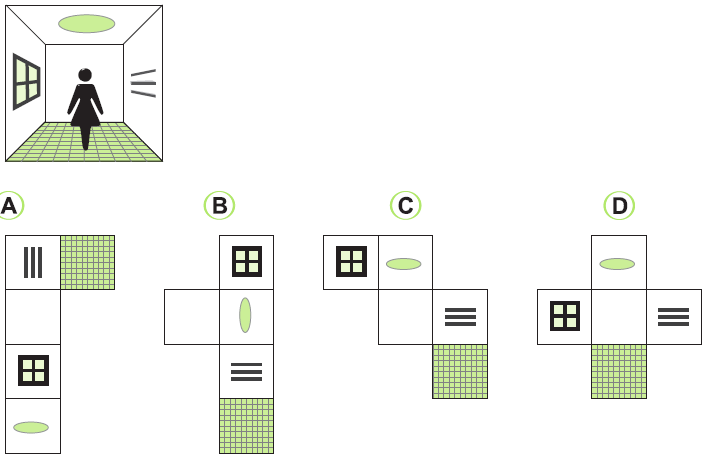
Riešenie:
Keď sa pozrieme na možnosť A, tak lampa sa nenachádza oproti podlahe, ale vedľa podlahy, čiže nevyhovuje možnosť A.
Zostavená izba podľa A:

Odpoveď: A
20. príklad
Zadanie:
V nepriehľadnom vrecúšku sú dve guľôčky biele, dve červené a dve modré. Najmenej koľko guľôčok musíme vytiahnuť z vrecúška, aby sme mali istotu, že medzi vytiahnutými guľôčkami bude aspoň 1 biela?
A: 6
B: 5
C: 4
D: 3
Riešenie:
Keď chceme mať istotu, že vytiahneme aspoň 1 bielu, tak musíme počítať s možnosťou, že bielu vytiahneme až na posledný možný pokus. teda najskôr vytiahneme všetky červené a modré (to sú 4 ťahy) a pri piatom ťahu už vytiahneme určite bielu.
Odpoveď: B
21. príklad
Zadanie:
Je daná trojica čísel: 53; 56,9 a 55,4. Určte číslo, ktoré musíme odčítať od najväčšieho z nich, aby aritmetický priemer novej trojice bol 54.
A: 2,9
B: 1,1
C: 4,3
D: 3,3
Riešenie:
najväčšie číslo …. 56,9
najväčšie číslo zväčšené o neznáme číslo … 56,9+x
Aritmetický priemer = súčet čísel : počet čísel
54 = (53 + 55,4 + 56,9+x) : 3 / .3
54 . 3 = (53 + 55,4 + 56,9+x)
162 = 165,3 + x / – 165,3
3,3 = x
Odpoveď: D
22. príklad
Zadanie:
V predajni mobilného operátora mali týždeň zliav. Mobilný telefón LF 34 zlacnel zo 769 € na 544 €. Približne o koľko percent klesla cena tohto mobilného telefónu?
A: 70,7
B: 58,6
C: 41,3
D: 29,3
Riešenie:
zľava …… 769 – 544 = 225 €
769 € ……………. 100%
225 € ………………… x%
769 . x = 100 . 225
769 . x = 22500 /769
x = 29,258… s presnosťou na 1 des. miesto 29,3
Odpoveď: D
23. príklad
Zadanie:
Rodičia a ich dve deti Anna a Boris sa rozhodli stráviť nedeľné popoludnie pri šachu, pričom mali v pláne hrať každý s každým jednu šachovú partiu. Rozhodnite, ktorí dvaja z nich neodohrali spoločnú partiu, ak viete, že:
- Anna vyhrala nad Borisom.
- Otec trikrát remizoval.
- Boris má na konte aj výhru, aj remízu, aj prehru.
Spoločnú partiu neodohrali:
A: otec a mama
B: Anna a otec
C: mama a Anna
D: Boris a mama
Riešenie:
Keďže každý s každým hral jednu partiu, tak každý z nich odohral 3 partie.
Označme ich otec (O), mama (M), Anna (A), Boris (B).
Z výrokov vyplýva, že Otec hral všetky zápasy, lebo 3-krát remizoval – OM, OA, OB.
Boris tiež hral všetky partie, lebo mal aj výhru, aj remízu, aj prehru – BO, BM, BA.
Z výrokov vyplýva, že Anna hrala s Borisom aj s otcom.
Spoločnú partiu teda neodohrali mama a Anna.
Odpoveď: C
24. príklad
Zadanie:
Osobný automobil prešiel trasu z Trenčína do Ružomberka za 1 hodinu 48 minút. Tieto dve mestá sú od seba vzdialené 144 km. O koľko minúť by si vodič skrátil spiatočnú cestu, ak by na nej prešiel za hodinu priemerne 90 km?
A: o 14 minút
B: o 12 minút
C: o 10 minút
D: o 8 minút
Riešenie:
v = 90 km/h
s = 144 km
t = ? h
t = s : v
t = 144 : 90
t = 1,6 h
1,6 h = 1 h + 0,6 h = 1 h + 0,6.60 min = 1 h 36 min
Z Trenčína do Ružomberka prešiel za 1 h 48 min, trasu si teda skrátil o 48 – 36 = 12 minút
Odpoveď: B
25. príklad
Zadanie:
Na obrázku vidíte trojuholník HRO. Ktorý z jeho vnútorných uhlov meria 65°?
A: žiadny
B: uhol HRO
C: uhol ROH
D: uhol OHR
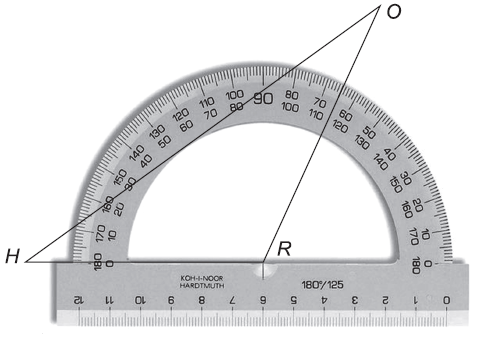
Riešenie:
Vďaka uhlomeru vieme, že veľkosť uhla HRO je 115°.
Súčet uhlov v trojuholníku je 180°.
180° – 115° = 65°
Zostávajúce 2 uhly majú spolu 65°. Ak by jeden z nich mal 65°, tak druhý by musel mať 0°. :) Preto správna odpoveď je A.
Odpoveď: A
26. príklad
Zadanie:
Pravouhlému trojuholníku ABC s odvesnami 5 cm a 12 cm je opísaná kružnica k. Vypočítajte dĺžku kružnice k v centimetroch. Pri výpočte použite π = 3,14 a výsledok zaokrúhlite na desatiny.
A: 81,6
B: 75,4
C: 40,8
D: 37,7
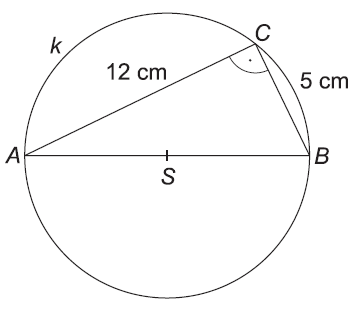
Riešenie:
Dĺžku kružnice vypočítame ako súčin jej priemeru a čísla pí.
o = d . π
Priemer kružnice d = AB.
AB je preponou pravouhlého trojuholníka ABC a jej dĺžku vypočítame pomocou Pytagorovej vety.
b = 12 cm
a = 5 cm
c = ? cm
c2 = a2 + b2
c2 = 52 + 122
c2 = 25 + 144
c2 = 169
c = druhá odmocnina zo 169 = 13 cm
Dĺžka kružnice o = d . π = 13 . 3,14 = 40,82 cm, čo je po zaokrúhlení na desatiny 40,8 cm.
Odpoveď: C
27. príklad
Zadanie:
Sieť na obrázku je tvorená zhodnými rovnostrannými trojuholníkmi. Ktorý zo štyroch zvýraznených útvarov má najväčší obsah?
A: lichobežník
B: kosodĺžnik
C: kosoštvorec
D: trojuholník

Riešenie:
Označme stranu rovnostranného trojuholníka a. Výšku rovnostranného trojuholníka v.
Obsah lichobežníka:
dlhšia základňa = 5a
kratšia základňa = 3a
výška = 2v
Obsah = ((5a + 3a) . 2v) : 2 = 16av : 2 = 8av
Obsah kosodĺžnika:
dlhšia strana = 4a
výška na dlhšiu stranu = 2v
Obsah = 4a . 2v = 8av
Obsah kosoštvorca:
strana = 3a
výška = 3v
Obsah = 3a . 3v = 9av
Obsah trojuholníka:
strana = 4a
výška na túto stranu = 4v
Obsah = (4a . 4v) : 2 = 16av : 2 = 8av
9av > 8av, preto má najväčší obsah kosoštvorec.
Odpoveď: C
28. a 29. príklad
Zadanie:
Na grafe je znázornený vývoj predaja elektromobilov v Nórsku, vo Francúzsku, v Nemecku a vo Veľkej Británii od roku 2013 do roku 2015.
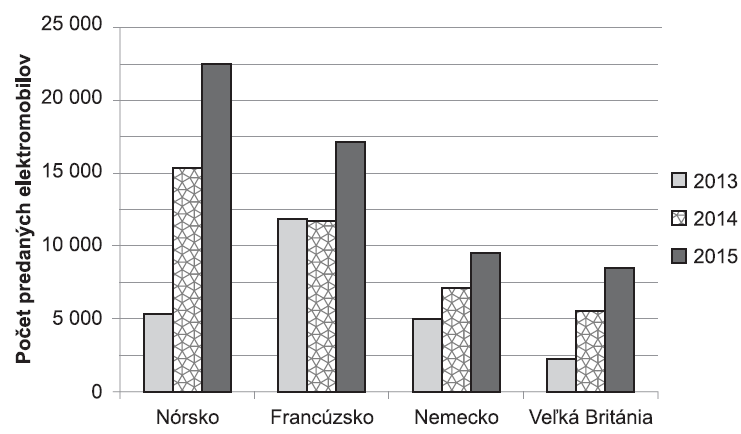
28. príklad
ZADANIE:
Približne koľko elektromobilov sa predalo podľa grafu vo Francúzsku v roku 2014?
A: 10 500
B: 11 500
C: 12 500
D: 13 500
RIEŠENIE:
Na obrázku nižšie si všimnite, ktorý stĺpec reprezentuje predaj vo Francúzsku v roku 2014.
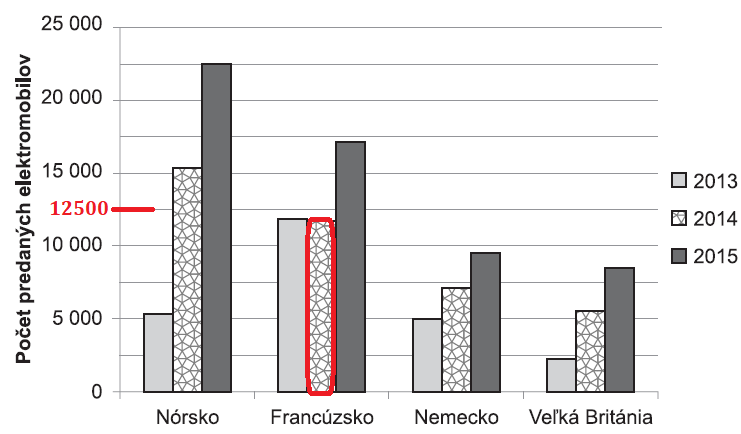
Všímame si, či je hodnota bližšie k 12 500 alebo k 10 000. Stĺpec zobrazuje hodnotu, ktorá je bližšie k 12 500, teda 11 500.
ODPOVEĎ: B
29. príklad
ZADANIE:
V ktorej krajine sa predalo iba v jednom z rokov 2013, 2014, 2015 viac elektromobilov, ako sa predalo v tom istom roku v Nórsku?
A: vo Veľkej Británii
B: vo Francúzsku
C: v Nemecku
D: v žiadnej krajine
RIEŠENIE:
Vo Francúzsku sa predalo viac elektromobilov ako v Nórsku iba v roku 2013.
V Nemecku sa nepredalo viac elektromobilov ako v Nórsku ani v jednom roku.
Vo Veľkej Británii sa nepredalo viac elektromobilov ako v Nórsku ani v jednom roku.
Vyhovuje teda Francúzsko.ODPOVEĎ: B
30. príklad
Zadanie:
Strýko Jonatán často zabúda svoje heslo. Ak však do šifrovacej mašinky znázornenej na obrázku vloží kartu so symbolmi a preklopí cez ňu hornú a ľavú časť, čierne kruhy mu prekryjú zbytočné symboly a zobrazí sa mu heslo.
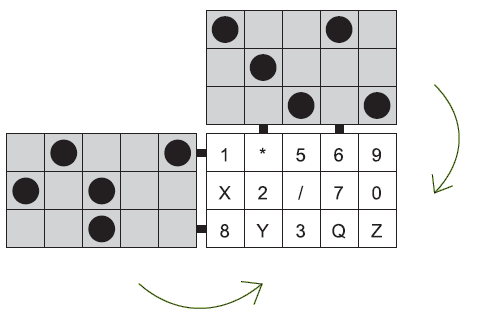
Označte možnosť, v ktorej sa po prekrytí zobrazí správne heslo.
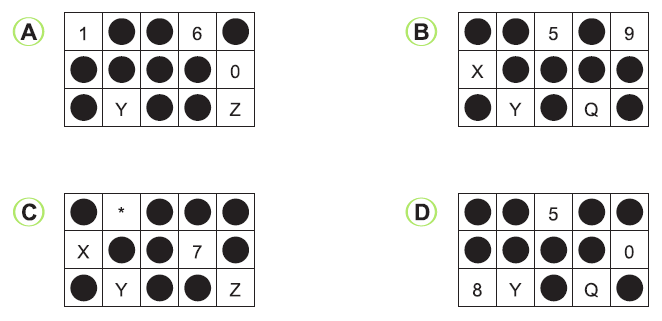
Riešenie:
Preklopenie si naznačíme červenými čiarami a zelenými krúžkami. Následne si žltou podfarbíme políčka, v ktorých zelený kruh nie je.
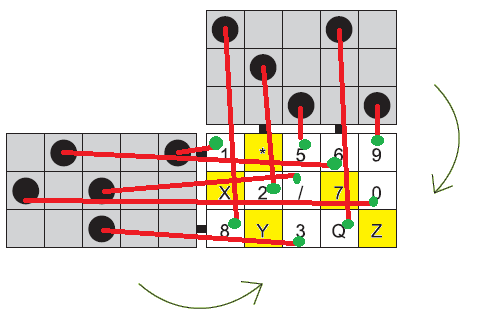
Vidíme, že z daných možností vyhovuje C.
