Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
Monitor 2022 matematika
1. príklad
Zadanie:
Na číselnej osi sú body A, B a C obrazmi reálnych čísel. Vypočítaj hodnotu výrazu A + B — C a výsledok zapíš v tvare desatinného čísla.
Riešenie:
Najskôr potrebujeme zistiť hodnotu 1 dielika:
- medzi číslom 0 a 1 je 5 dielikov, preto 1 dielik = 1 : 5 = 0,2
Teraz ľahko zistíme hodnoty A, B, C:
- A = -2 . 0,2 = -0,4
- B = 2 . 0,2 = 0,4
- C = 1 + 3 . 0,2 = 1,6
Vypočítame hodnotu výrazu:
- A + B – C = -0,4 + 0,4 – 1,6 = -1,6
Odpoveď: -1,6
2. príklad
Zadanie:
Veľkosť uhla DVC na obrázku je tretinou veľkosti uhla BVC. Polpriamka VE je os uhla AVC. Body A, V, B ležia na jednej priamke. Vypočítaj v stupňoch veľkosť uhla γ.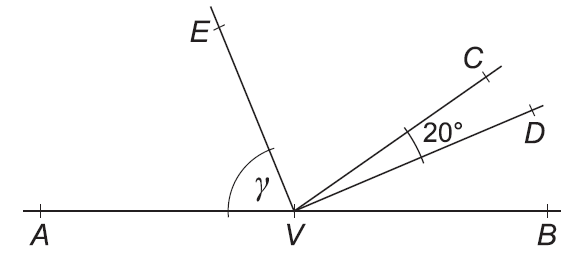
Riešenie:
Ak veľkosť DVC je tretinou uhla BVC, potom veľkosť uhla BVC = 3 . 20° = 60°
Keďže polpriamka VE je osou uhla AVC, tak uhol gama je polovicou uhla AVC. Potrebujeme teda vypočítať veľkosť uhla AVC.
Súčet uhlov AVC a BVC je uhol priamy, teda 180°.
|∠AVC|+|∠BVC| = 180°
|∠AVC|+60° = 180° / -60°
|∠AVC| = 120°
Teraz ľahko vypočítame veľkosť uhla gama:
γ = |∠AVC| : 2
γ = 120° : 2
γ = 60°
Odpoveď: 60
3. príklad
Zadanie:
Desiati priatelia sa dohodli, že si objednajú pizze spolu, aby využili akciu, kedy dostanú každú štvrtú pizzu za polovicu. Jedna celá pizza stoji 6 €. Koľko eur ich vyšla 1 pizza, ak si objednali 10 pízz? Výsledok uveď s presnosťou na desatiny.
Riešenie:
1 pizza … 6 €
Každá 4. pizza je za polovicu, teda 6:2 = 3 € – každá 4. v tomto prípade bude 4. a 8. pizza
Priateľov je 10, preto 2 pizze boli po 3 € a 8 pízz po 6 €.
Spolu … 2 . 3 + 8 . 6 = 6 + 48 = 54 €
Cena 1 pizze: 54 : 10 = 5,4 €
Odpoveď: 5,4
4. príklad
Zadanie:
V materskej škole chcú zasiať trávu na pozemok okolo pieskoviska, ktoré má pôdorys v tvare štvorca s výmerou 49 m². Umiestnené je na štvorcovom pozemku so stranou dlhou 9 m tak, ako to vidíme na obrázku. Koľko celých balení trávnikovej zmesi treba kúpiť na zatrávnenie plochy pozemku okolo pieskoviska, ak jedno balenie stačí na 5 m² plochy?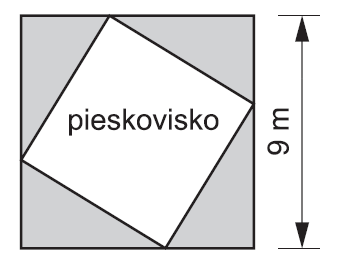
Riešenie:
pieskovisko … S1 = 49 m²
pozemok ……. tvaru štvorca so stranou 9 m, preto S = a . a = 9 . 9 = 81 m²
trávnik ………. S2 = ? m²
trávnik …….. S2 = S – S1 = 81 – 49 = 32 m²
na 5 m² trávnika ……… 1 balenie tráv. zmesi
na 32 m² trávnika …….. x balení tráv. zmesi
…ide o priamu úmernosť…
32 . 1 = 5 . x
x = 32 : 5
x = 6,4 tzn. 7 celých balení tráv. zmesi
Odpoveď: 7
Zadanie Bludisko
V mobilnej aplikácii Bludisko sa po každom kliknutí zvolený štvorec otočí o 90° v smere chodu hodinových ručičiek.
Na zadanie Bludisko sa vzťahujú úlohy 5 a 6.
5. príklad
Zadanie:
Minimálne koľko kliknutí je potrebné urobiť, aby sa bludisko na obrázku vľavo zmenilo na bludisko vpravo?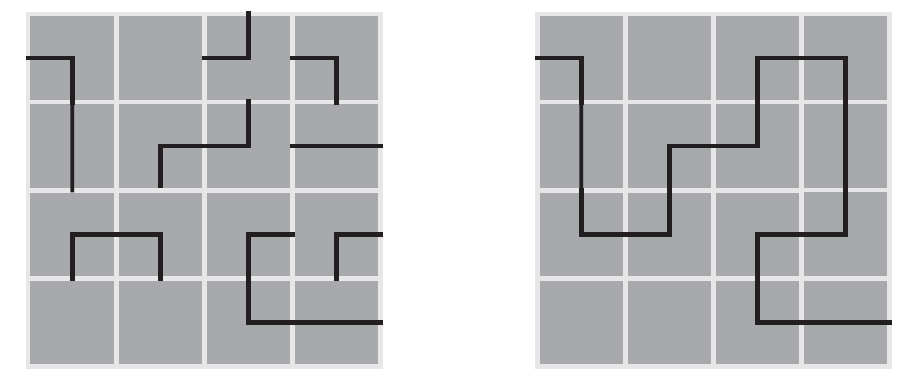
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 9
6. príklad
Zadanie:
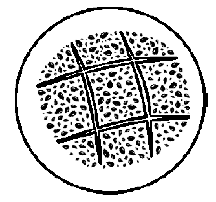
Vypočítaj dĺžku cesty v bludisku zvýraznenú čiernou farbou, ak dĺžka strany štvorca je 7 mm. Výsledok uveď v milimetroch.
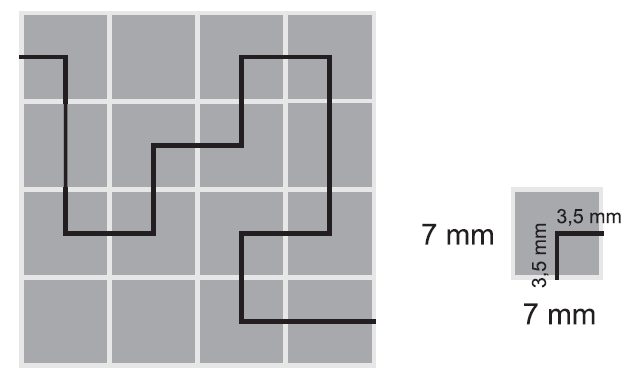
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 91
7. príklad
Zadanie:
Pravidelný osemuholník so stranou dlhou 10 cm vznikol tak, že sme z papierového štvorca odstrihli v jeho vrcholoch rovnoramenné trojuholníky. Vypočítaj dĺžku strany pôvodného štvorca v centimetroch. Výsledok zaokrúhli na celé číslo.
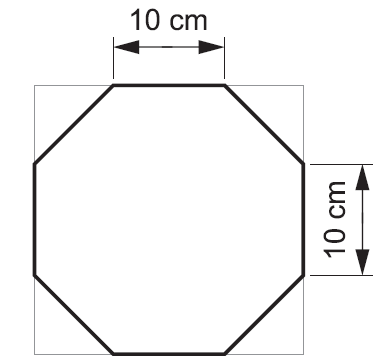
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 24
8. príklad
Zadanie:
Patrik mal za úlohu vypísať všetky trojciferné čísla zložené z číslic 0, 2, 5 a 8 bez opakovania, Podarilo sa mu nájsť tieto čísla: 205, 502, 805, 802, 520, 820, 850, 250. Koľko čísel mu chýba?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 10
9. príklad
Zadanie:
Na číselnej osi je vyznačených šesť rovnako dlhých úsekov. Bod A je obrazom reálneho čísla. Zapíš toto číslo zlomkom v základnom tvare.
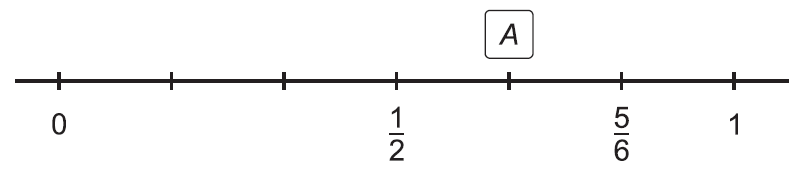
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 2/3
10. príklad
Zadanie:
V triede je 20 žiakov. Každý z nich pripravil projekt z geografie. Na hodine vždy vyžrebujú jedného žiaka z tých, ktorí ešte svoj projekt neprezentovali, aby ho prezentoval na nasledujúcej hodine. Aká je pravdepodobnosť, že vyberú Petra, ak 13 jeho spolužiakov už svoj projekt prezentovalo? Výsledok zapíš zlomkom v základnom tvare.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 1/7
11. príklad
Zadanie:
V bytovom dome býva 60 rodín. Kruhový diagram znázorňuje percentuálne zastúpenie počtu rodín podľa počtu áut v rodine. Koľko rodín má najmenej dve autá?
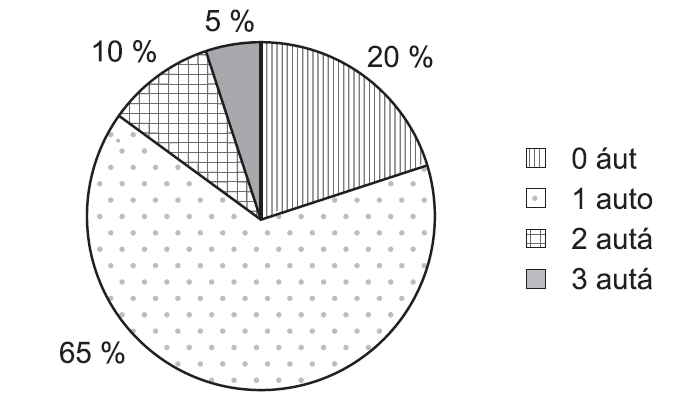
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 9
12. príklad
Zadanie:
Do každého pecňa chleba pridávajú v miestnej pekárni slnečnicové, ľanové, konopné a tekvicové semienka v pomere 5 : 3 : 4 : 2. Koľko kilogramov slnečnicových semienok treba ešte pridať, ak ľanové, konopné a tekvicové semienka majú spolu hmotnosť 6,3 kg?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 3,5
13. príklad
Zadanie:
Nájdi číslo, ktoré je riešením rovnice 6x — (2 — 2x) = 3 • (x — 4).
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: -2
Zadanie Zámková dlažba
Zámková dlažba Pán Jaroslav chce vydláždiť zámkovou dlažbou časť pozemku popri chate. Dlaždice sú v tvare kvádra s rozmermi podstavy 20 cm a 10 cm a výškou 10 cm. Rozmery vydláždenej časti, jej umiestnenie pri chate a okolitom trávniku sú znázornené na obrázku.
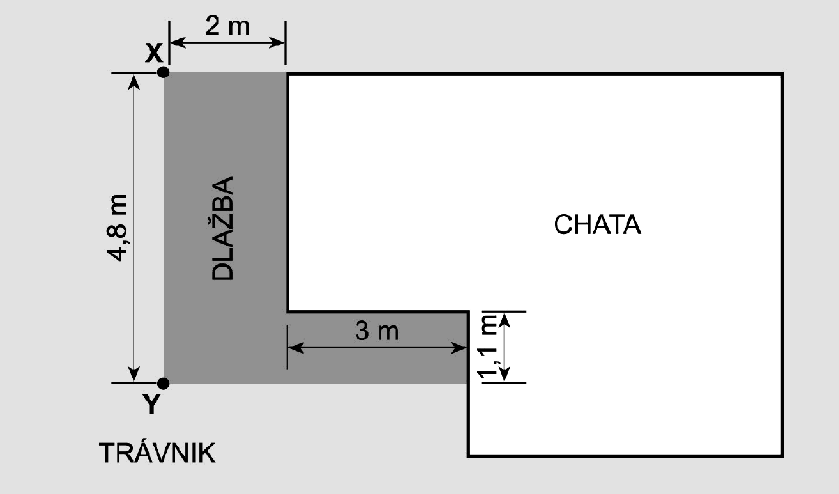
Na zadanie Zámková dlažba sa vzťahujú úlohy 14 až 16.
14. príklad
Zadanie:
Z miesta, kde má byt‘ zámková dlažba, treba najskôr odstrániť zeminu do hĺbky 0,2 m. Koľko metrov kubických zeminy treba odstrániť? Výsledok napíš s presnosťou na dve desatinné miesta.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 2,58
15. príklad
Zadanie:
Medzi dlažbu a trávnik treba umiestniť obrubníky. Jeden obrubník je dlhý 1 m. Koľko kusov obrubníkov musí pán Jaroslav kúpiť?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: 12
16. príklad
Zadanie:
Pri kladení zámkovej dlažby sa začína v bode X. Dlažba sa bude ukladať podľa vzoru, ktorý je znázornený na obrázku. Niekedy treba dlaždice prepíliť.
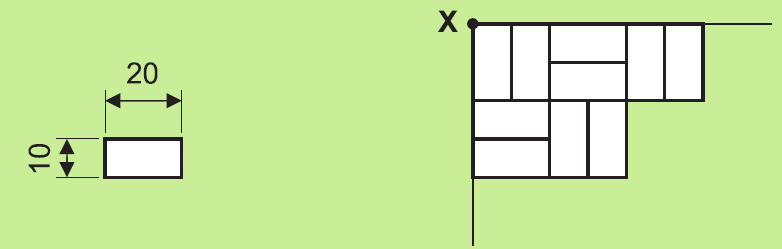
Ako bude vyzerať dlažba uložená v rohu, ktorý je na obrázku v zadaní označený ako bod Y?
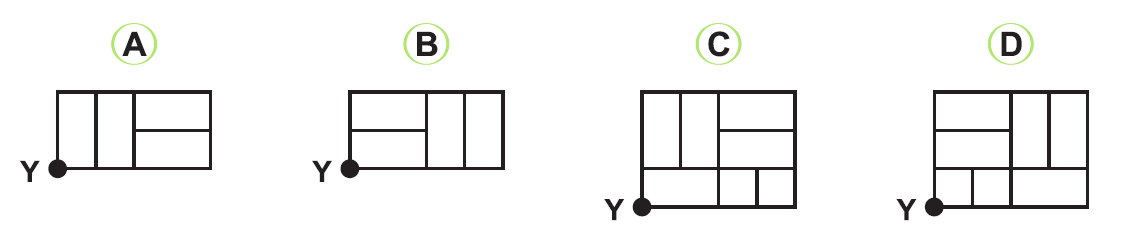
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: B
17. príklad
Zadanie:
Novákovci plánujú v priebehu septembra opraviť fasádu domu, S prácami sa začne 2. septembra, Počas nedieľ a sviatkov sa pracovať nebude. Tieto dni sú v kalendári podčiarknuté.
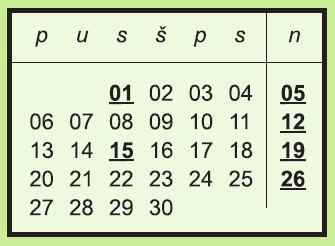
Štyria robotnici by opravili fasádu za 10 dní. Kedy možno očakávať skončenie prác, ak budú pracovať len dvaja robotníci? Predpokladáme, že všetci pracujú rovnako výkonne.
A: 6. septembra
B: 7. septembra
C: 21. septembra
D: 25. septembra
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: D
18. príklad
Zadanie:
Ktorá z nasledujúcich nerovností platí?
Nerovnosť 1: 3² > 2³ Nerovnosť 2: (-3)² < (-2)³
A: Platí len nerovnosť 1.
B: Platí len nerovnosť 2.
C: Obidve nerovnosti platia.
D: Ani jedna nerovnosť neplati.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: A
19. príklad
Zadanie:
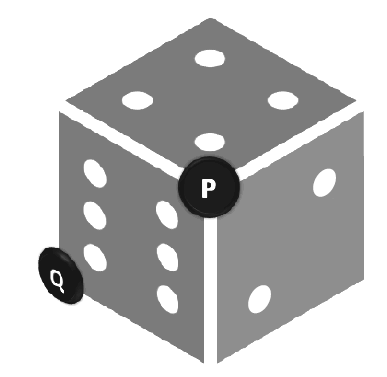
Súčet hodnôt na protiľahlých stenách hracej kocky je vždy 7. Súčet hodnôt troch stien kocky so spoločným vrcholom P je 12. Koľko je súčet hodnôt troch stien kocky so spoločným vrcholom Q?
A: 9 B: 10 C: 12 D: 14
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: D
20. príklad
Zadanie:
Linda robila prieskum medzi žiakmi svojej školy. Pýtala sa ich, či majú v rodine len brata alebo len sestru, alebo oboje, alebo sú bez súrodenca. Počet jednotlivých odpovedí zhrnula do tabuľky.
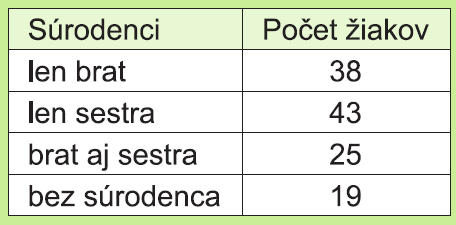
Posúď pravdivosť nasledujúcich dvoch tvrdení:
1. Linda zistila, že bez súrodenca je viac ako 10% opýtaných žiakov.
2. U pätiny opýtaných žiakov sú v rodine určite najmenej tri deti.
Pravdivé
A je len prvé tvrdenie.
B je len druhé tvrdenie.
C nie je žiadne z tvrdení.
D sú obidve tvrdenia.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: D
21. príklad
Zadanie:
Pani Šťastná sa počas týždňa vážila so svojím bábätkom. Namerané hodnoty sú uvedené v nasledujúcom grafe v kilogramoch.
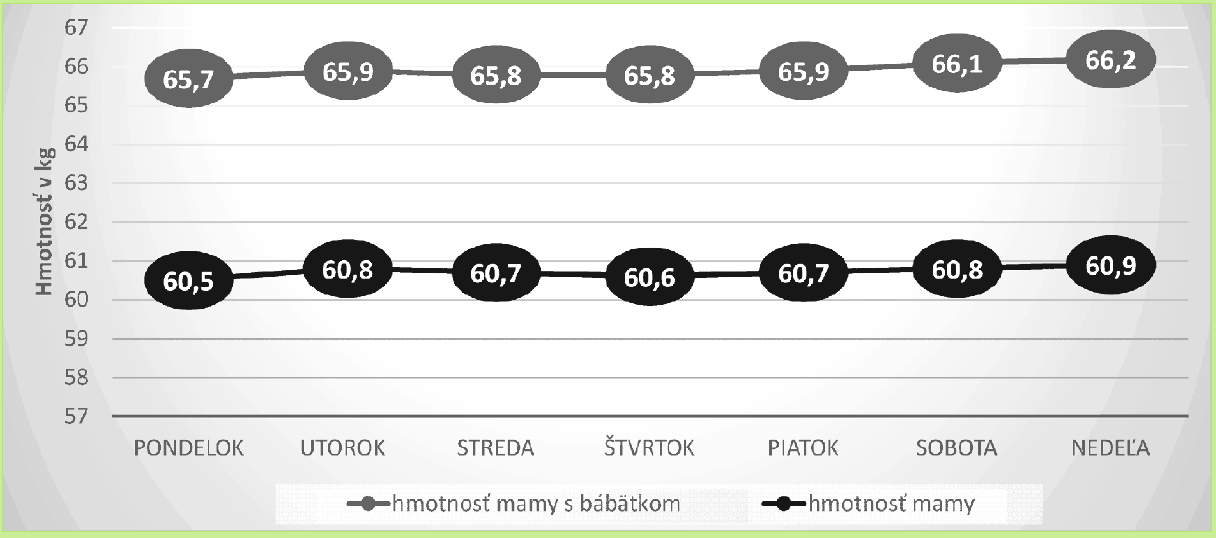
O koľko kilogramov bola hmotnosť bábätka väčšia v nedeľu ako v pondelok?
A: 0,1 kg
B: 0,2 kg
C: 0,3 kg
D: 0,4 kg
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: A
22. príklad
Zadanie:
Číslo je dokonalé vtedy, ak je súčet všetkých jeho deliteľov okrem čísla samotného rovnaký ako toto číslo.
Napríklad číslo 28 je dokonalé. Súčet jeho deliteľov 1, 2, 4, 7 a 14 je 28.
Ktoré z nasledujúcich čísel je tiež dokonalé?
A: 14 B: 12 C: 8 D: 6
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: D
23. príklad
Zadanie:
Riadky tabuľky sú označené písmenami R, S, T a stĺpce číslami 1, 2, 3. Do výrazu R2 — S3 + T1 dosaď príslušné čísla a vypočítaj jeho hodnotu.
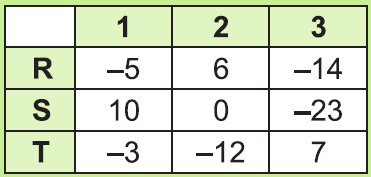
V ktorej možnosti je uvedený správny výsledok?
A: -14 B: -20 C: 26 D: 32
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: C
24. príklad
Zadanie:
Ktoré číslo nie je riešením nasledujúcej nerovnice?
3 < 2 ⋅ (3x – 9)
A: 6 B: 5 C: 4 D: 3
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: D
25. príklad
Zadanie:
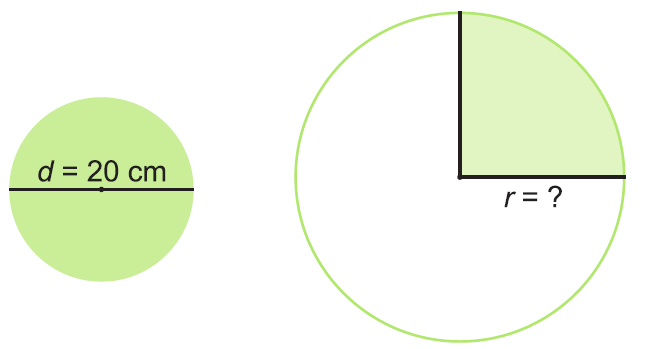
Menší kruh a štvrtina väčšieho kruhu majú rovnaký obsah. Vypočítaj polomer väčšieho kruhu v cm, ak priemer menšieho kruhu je 20 cm. Počítaj s hodnotou π = 3,14.
A: 10 B: 20 C: 40 D: 80
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: B
26. príklad
Zadanie:
Ku každému plánu stavby z kociek (P1 až P3) treba priradiť pohľad na stavbu spredu (nárys).
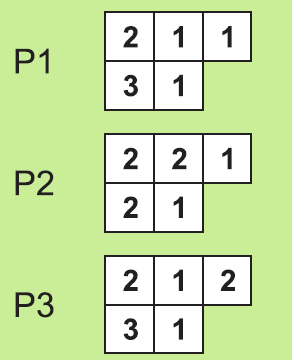
Ktorý z nárysov A, B, C alebo D nepoužijeme?
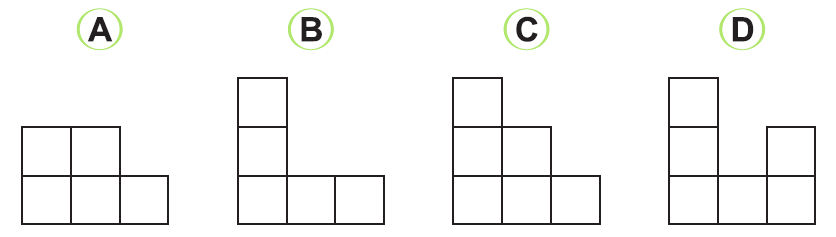
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: C
27. príklad
Zadanie:
Osoba na obrázku meria približne 170 cm. Približne koľko meria priemer kmeňa zrezaného stromu v mieste, kde sa ho osoba dotýka?

Priemer kmeňa stromu je približne:
A: 1,3 m B: 150 cm C: 9 dm D: 600 mm
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: C
28. príklad
Zadanie:
V nasledujúcej tabuľke je uvedený cenník lístkov kúpaliska.

Počas dňa si lístok na celodenné kúpanie zakúpilo x dospelých a y detí. Na popoludňajšie kúpanie sa predalo 17 lístkov. Ktorý výraz vyjadruje tržbu kúpaliska počas celého dňa?
A: 6,5xy + 17
B: 4x + 2,5y + 17
C: 4x + 2,5y + 34
D: 6,5xy + 34
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: C
29. príklad
Zadanie:
Do škatuľky v tvare kvádra so štvorcovou podstavou so stranou dĺžky 4 cm a výškou 5 cm nasypeme čaj 1 cm pod horný okraj. Do druhej škatuľky v tvare kvádra s rozmermi podstavy 5 cm a 4 cm a výškou 4 cm nasypeme ten istý druh čaju, rovnako 1 cm pod horný okraj. Vypočítaj rozdiel v objeme nasypaných čajov v centimetroch kubických.
Rozdiel je:
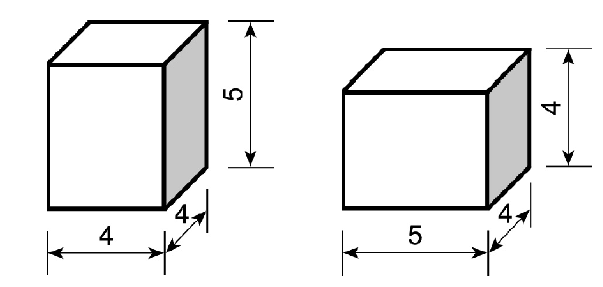
A: 0 B: 1 C: 4 D: 2
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Odpoveď: C
30. príklad
Zadanie:
V obci stojí vedľa seba päť kontajnerov na triedený odpad. Každý z nich má inú farbu podľa toho, čo sa v ňom zbiera. Na základe nasledujúcich tvrdení zisti, akú farbu má kontajner, ktorý sa nachádza uprostred.
1. žltý kontajner je hneď napravo od oranžového kontajnera.
2. Zelený a modrý kontajner nie sú vedľa seba.
3. Medzi oranžovým a modrým kontajnerom je iba červený kontajner.
Kontajner, ktorý sa nachádza uprostred, má farbu
A: oranžovú B: zelenú C: červenú D: modrú
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
