Vyriešený test z Testovania 9 – T9-2015

Príklad č. 1

Vypočítajte a výsledok zapíšte desatinným číslom zaokrúhleným na dve desatinné miesta.

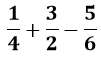
Riešenie:

 

• najskôr je potrebné nájsť spoločného menovateľa, čiže najmenší spoločný násobok čísel 4, 2, 6;
  n(2, 4, 6) = 12;
• potom podiel „spoločný menovateľ / menovateľ“ násobíme čitateľom, napr. 12 : 4 = 3, čiže zapíšeme 3 . 1;
• následne čitateľ zjednodušíme;
• zlomok 11/12 upravíme na desatinné číslo;
• na mieste tisícin je číslica 6, tak zaokrúhlime smerom nahor;

Výsledok: 0,92

---

Príklad č. 2

Vypočítajte súčin číselných výrazov A a B, ak
A=10-(9-8)-(6-7)
B=4⋅10²+5⋅10+9

Riešenie:

A⋅B = (10-(9-8)-(6-7))⋅(4⋅10²+5⋅10+9)
= (10-(1)-(-1))⋅(4⋅100+50+9)
= (10-1+1)⋅(400+59)
= 10⋅459
= 4590
 

• príklad môžeme riešiť tak, že najskôr si vypočítame hodnotu výrazov A a B a nakoniec ich vynásobíme;
• nezabudnite, ak je „mínus“ pred zátvorkou, po odstránení zátvorky sa výraz vo vnútri zátvorky mení na opačný napr. -(-1) = +1 .

Výsledok: 4590

---

Príklad č. 3

Na základe informácií uvedených v tabuľke zistite, o koľko kilometrov je celková dĺžka zjazdoviek v Tatranskej Lomnici väčšia ako celková dĺžka zjazdoviek na Štrbskom Plese.

Lyžiarske stredisko	Dĺžka zjazdovky podľa obťažnosti
	ľahká	stredne ťažká	ťažká
Tatranská Lomnica	5 350 m	5 190 m	1 240 m
Starý Smokovec	3 375 m	0 m	0 m
Štrbské Pleso	2 590 m	5 600 m	0 m

Riešenie:

• zjazdovky v Tatranskej Lomnici ……….. 5 350 + 5 190 + 1 240 = 11 780 m
• zjazdovky na Štrbskom Plese ……….. 2 590 + 5 600 + 0 = 8 190 m
• hodnoty odčítame ……….. 11 780 – 8 190 = 3 590 m = 3,59 km
• celková dĺžka zjazdoviek v Tatranskej Lomnici je o 3,59 km väčšia ako celková dĺžka zjazdoviek na Štrbskom Plese

Výsledok: 3,59

---

Príklad č. 4

Ktoré číslo je na číselnej osi rovnako vzdialené od čísel 299 a 1 051?

Riešenie:

• hľadané číslo sa musí nachádzať v strede medzi číslami 299 a 1051, preto
• najskôr odčítame dané čísla (väčšie číslo – menšie číslo)
  1 051 – 299 = 752
• následne dané číslo vydelíme dvomi
  752 : 2 = 376
• hľadané číslo získam pripočítaním výsledku k menšiemu z daných čísel
  299 + 376 = 675
• graficky:

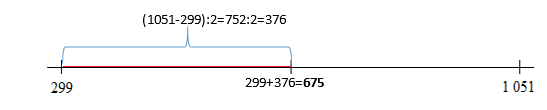
Výsledok: 675

---

Zadanie: VÝSLEDKY TESTU

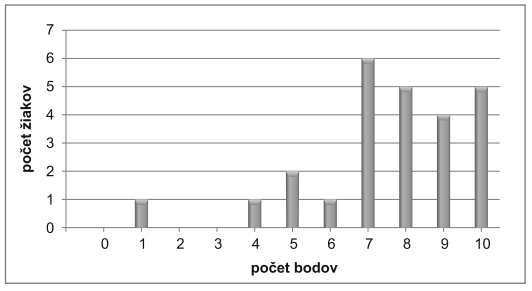
Žiaci 9.A triedy písali test, v ktorom mohol každý získať najviac 10 bodov. Rozdelenie žiakov 9. A triedy podľa počtu bodov získaných v teste je uvedené v nasledujúcej tabuľke.

Počet bodov	0	1	2	3	4	5	6	7	8	9	10
Počet žiakov	0	1	0	0	1	2	1	6	5	4	5

K zadaniu VÝSLEDKY TESTU sa vzťahujú úlohy č. 5 a č. 6.

Príklad č. 5

Koľko žiakov 9. A triedy získalo v teste menej bodov, ako je priemerný počet bodov získaný všetkými žiakmi triedy?

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 11

---

Príklad č. 6

Adam získal 6 bodov. Údaje uvedené v tabuľke spracoval do stĺpcového diagramu. Stĺpec znázorňujúci počet žiakov s 10 bodmi mal výšku 7,5 cm. Vypočítajte, koľko centimetrov vysoký bol stĺpec znázorňujúci počet žiakov so 7 bodmi.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 9

---

Príklad č. 7

Na obrázku sú znázornené 4 priamky a ich vzájomná poloha. Vypočítajte veľkosť uhla β v stupňoch.

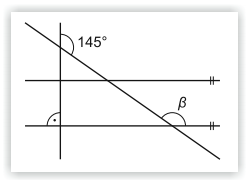
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 125

---

Príklad č. 8

Najviac koľko kociek s hranou dĺžky 5 cm môže vložiť Lenka do škatule tvaru kocky s vnútornou hranou dĺžky 0,4 m?

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 512

---

Príklad č. 9

Vypočítajte obsah plášťa 5-bokého hranola, ak povrch hranola je 258 cm² a jedna podstava hranola má obsah 64,6 cm². Výsledok uveďte v cm² v tvare desatinného čísla.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 128,8

---

Príklad č. 10

Koľko je všetkých párnych dvojciferných čísel, ktoré sa dajú vytvoriť z číslic 2, 4 a 7? Číslice sa vo vytvorenom čísle môžu opakovať.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: 6

---

Zadanie: Nákup darčekov

V tabuľke sú uvedené údaje o Milanových výdavkoch za darčeky v minulom roku.

K zadaniu Nákup darčekov sa vzťahujú úlohy č. 11 a 12.

Príklad č. 11

Ktorý kruhový diagram správne zobrazuje rozdelenie Milanových výdavkov za darčeky?

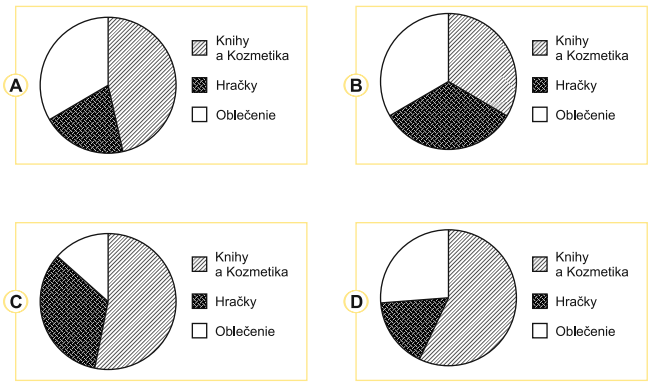
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: D

---

Príklad č. 12

Tento rok Milan plánuje znížiť výdavky za darčeky o 15% oproti minulému roku. Koľko eur plánuje Milan minúť na darčeky tento rok?
A: 127,50 €
B: 135,00 €
C: 148,50 €
D: 140,00 €

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: A

---

Príklad č. 13

13. Skupina troch dievčat vyhrala v prírodovednej súťaži 30 eur. Kamila, Magda a Zuzka si výhru rozdelili podľa svojich výkonov v pomere 3:4:5. Ktorá z možností je nesprávna?
A. Kamila a Magda majú spolu viac eur ako Zuzka.
B. Zuzka a Kamila majú spolu 20 €.
C. Magda a Zuzka majú spolu o 16 € viac ako Kamila.
D. Kamila má o 5 € menej ako Zuzka.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: C

---

Príklad č. 14

Po zdražení o 40% stál zápisník 10,50 €. Koľko eur by stál tento zápisník, keby namiesto o 40% zdražel len o 20%.
A. 8,40 €
B. 9,00 €
C. 7,56 €
D. 8,75 €

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: B

---

Príklad č. 15

Ktoré číslo má tú vlastnosť, že keď ho zväčšíme o 7, dostaneme číslo, ktoré má rovnakú absolútnu hodnotu ako pôvodné číslo?
A. 3,5
B. -3,5
C. -7
D. -14

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: B

---

Príklad č. 16

Daný je štvorec s dĺžkou strany 6 cm a obdĺžnik s dĺžkami strán 5 cm a 4 cm. Žiaci vypočítali obvod a obsah daných útvarov a vyslovili dve tvrdenia.
1. Obvod štvorca je o 6 cm väčší ako obvod obdĺžnika.
2. Obsah štvorca je 1,8-krát väčší ako obsah obdĺžnika.
Posúďte pravdivosť týchto dvoch tvrdení a vyberte správnu možnosť.
A. Obidve tvrdenia sú pravdivé.
B. Prvé tvrdenie je pravdivé, druhé je nepravdivé.
C. Prvé tvrdenie je nepravdivé, druhé je pravdivé.
D. Obidve tvrdenia sú nepravdivé.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: A

---

Príklad č. 17

Anka si kúpila na výlet 1,5 litra minerálky a tri pätiny z nej vypila. Vyberte pravdivé tvrdenie.
A. Vypila menej ako polovicu.
B. Zostalo je 6dl minerálky.
C. Vypila viac ako 1 liter minerálky.
D. Zostali jej dve tretiny minerálky.

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: B

---

Príklad č. 18

Dĺžky strán dvoch trojuholníkov sme zoradili podľa veľkosti: 8 cm,
10 cm, 13 cm, 15 cm, 17 cm, 19 cm. Jeden z týchto trojuholníkov je pravouhlý. Vypočítajte obvod tohto pravouhlého trojuholníka v centimetroch.
A. 31
B. 33
C. 40
D. 42

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: C

---

Príklad č. 19

Nad každou dvojicou vedľa seba zobrazených výrazov na obrázku je ich súčet. Zistite, ktorý výraz bude na najvyššom mieste na obrázku.
A. 2a + 3B. 9a + 1C. 6a + 9D. 2a + 9

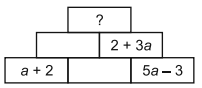
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: D

---

Príklad č. 20

Obsah štvoruholníka ABCD znázorneného v štvorcovej sieti sa rovná:
A: 22 cm²
B: 24 cm²
C: 28 cm²
D: 56 cm²

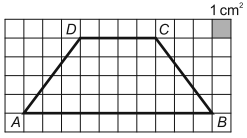
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)

Výsledok: C

---

Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.