Príklad č. 1
800 – 700 : 2 + 100 ⋅ 15,67
Riešenie:
800 – 700 : 2 + 100 ⋅ 15,67 = 800 – 350 + 1567 = 2 017
Výsledok: 2017
Príklad č. 2
Na číselnej osi sú znázornené čísla M, A, V. Vypočítajte M + A + V.

Riešenie:
M = -0,07
A = 0,08
V = 0,16
M + A + V = -0,07 + 0,08 + 0,16 = 0,17
Výsledok: 0,17
Príklad č. 3
Vyriešte rovnicu a výsledok uveďte v tvare desatinného čísla s presnosťou na stotiny.
11 ⋅ (x – 1) = 11 – (1 + x)
Riešenie:
11 ⋅ (x – 1) = 11 – (1 + x)
11x – 11 = 11 – 1 – x
11x – 11 = 10 – x /+x +11
12x = 21 /:12
x = 1,75
Výsledok: 1,75
Príklad č. 4
Vypočítajte.
(–0,7)2 ⋅ 102 + (–0,2 ⋅ 10)3 =
Riešenie:
(–0,7)2 ⋅ 102 + (–0,2 ⋅ 10)3 = 0,49 ⋅ 100 + (-2)3 = 49 + (-8) = 41
Výsledok: 41
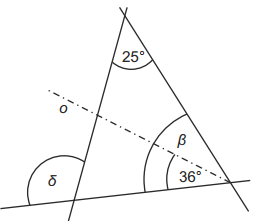
Príklad č. 5
Polpriamka o znázornená na obrázku je osou uhla β. Vypočítajte veľkosť uhla δ v stupňoch.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 97°
Príklad č. 6
10 gramov kivi obsahuje rovnaké množstvo vitamínu C ako 50 gramov pomarančov. 100 gramov šípok obsahuje rovnaké množstvo vitamínu C ako 200 gramov kivi. Koľko gramov pomarančov obsahuje rovnaké množstvo vitamínu C ako 50 gramov šípok?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 500
Príklad č. 7
Všetci žiaci zo štyroch tried 9. ročníka základnej školy sa zapojili do zberu papiera. V tabuľke sú uvedené informácie o počte týchto žiakov a o priemernom množstve nazbieraného papiera v kilogramoch na jedného žiaka v triede. O koľko kilogramov papiera menej nazbierali žiaci 9. D ako žiaci 9. B?

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 40
Príklad č. 8
Zistite, koľko rôznych štvorciferných čísel môžeme vytvoriť z číslic 3 a 8 tak, aby v každom vytvorenom štvorcifernom čísle boli použité dve číslice 3 a dve číslice 8.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 6
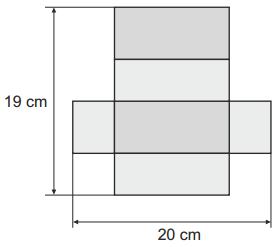
Príklad č. 9
Kváder, ktorého sieť je zobrazená na obrázku, má dva rozmery 11 cm a 4,5 cm. Vypočítajte v centimetroch tretí rozmer tohto kvádra.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 5
Príklad č. 10
V recepte na lečo sa odporúča zmiešať paradajky, papriku a cibuľu v pomere 4 : 3 : 1. Pani kuchárka už pripravila cibuľu aj papriku, pričom cibule bolo o päť kg menej ako papriky. Koľko kg paradajok bude potrebovať podľa tohto receptu?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 10
Príklad č. 11
Karol si šetril na tablet. Keď mal ušetrených 178 € zistil, že cenu tabletu znížili o 25 %, takže si ho môže hneď kúpiť a ešte mu z ušetrených peňazí zostane 13 €. Koľko eur stál tablet pred zlacnením?
A: 206,25
B: 191,00
C: 220,00
D: 225,50
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Príklad č. 12
Na školskom výlete bolo x chlapcov. Dievčat bolo o 6 menej ako chlapcov. Dvojsedačkovou lanovkou sa všetci vyviezli z dolnej na hornú stanicu. Rozhodnite, ktorý výraz vyjadruje počet dvojsedačiek obsadených žiakmi, ak každá bola obsadená dvomi žiakmi.
A: (x – 6) : 2
B: (x – 6 + x – 6) : 2
C: (x + x) : 2 – 6
D: (x + x – 6) : 2
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 13
Z čísel uvedených na kartičkách sčítajte najväčšie a najmenšie číslo.

A: 3,41
B: 3,30
C: 3,21
D: 3,10
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 14
Na tácke boli marhuľové a slivkové koláče v pomere 3 : 2. Po zjedení troch marhuľových koláčov je šanca vybratia slivkového aj marhuľového koláča rovnaká. Koľko koláčov bolo na začiatku spolu na tácke?
A: 5
B: 8
C: 10
D: 15
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 15
Dokreslením bodu F a dvoch úsečiek EF, FG vznikne v pravouhlej sústave súradníc rovnoramenný lichobežník EFGH so základňami EF a GH. Aké súradnice má bod F, ak bod G má súradnice [2; –1].
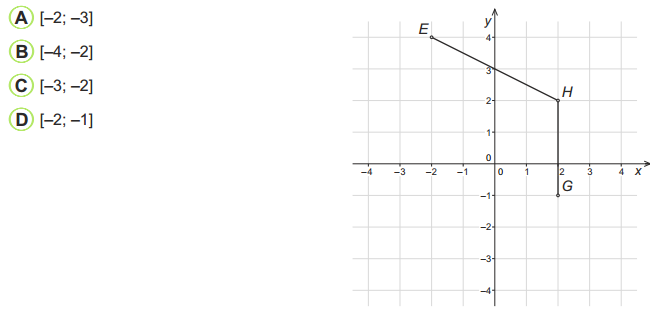
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 16
Kruh K má polomer 130 mm a kruh L má priemer 50 mm. O koľko milimetrov je obvod kruhu K väčší ako obvod kruhu L? Výsledok zaokrúhlite na celé číslo. Pri výpočtoch použite hodnotu π= 3,14.
A: o 188
B: o 251
C: o 502
D: o 659
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 17
Stela si prečítala v miestnej tlači:
„V januári napadalo viac zrážok ako vo februári. V apríli napadalo menej zrážok ako vo februári. V máji napadalo viac zrážok ako v marci, aj ako v januári. V marci napadalo menej zrážok ako v januári, ale viac ako vo februári.“
Na základe týchto informácií Stela uviedla dve tvrdenia:
1. Najmenej zrážok napadalo vo februári.
2. Najviac zrážok napadalo v máji.
Posúďte pravdivosť oboch Steliných tvrdení a vyberte správnu možnosť.
A: Obidve tvrdenia sú pravdivé.
B: Len prvé tvrdenie je pravdivé.
C: Len druhé tvrdenie je pravdivé.
D: Obidve tvrdenia sú nepravdivé.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
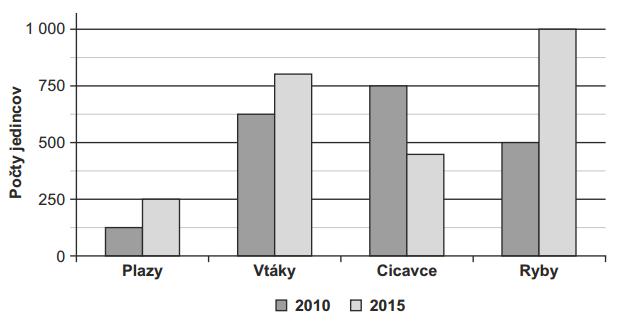
Zadanie ZOOLOGICKÁ ZÁHRADA (ZOO)
Minulý rok v II. polroku navštívilo zoologickú záhradu 181 003 ľudí, čo bolo o 20 145 ľudí viac ako v I. polroku.
Na ploche 400 000 štvorcových metrov chovajú štyri skupiny živočíchov: plazy, vtáky, cicavce a ryby.
Stĺpcový diagram znázorňuje počty jedincov, ktoré chovali v ZOO na konci uvedených rokov podľa skupín živočíchov.
Príklad č. 18
Koľko ľudí navštívilo túto zoologickú záhradu v minulom roku?
A: 201 148
B: 321 716
C: 341 861
D: 382 151
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Príklad č. 19
Koľko hektárov zaberá v tejto zoologickej záhrade plocha, na ktorej sú chované živočíchy?
A: 40
B: 400
C: 4 000
D: 40 000
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 20
Na základe údajov zobrazených v diagrame zistite, približne koľko jedincov spolu chovali v tejto zoologickej záhrade na konci roku 2015.
A: 2 800
B: 2 500
C: 2 300
D: 2 000
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
