Úlohy pokrývajú jednotlivé tematické celky matematiky základnej školy tak, aby vaša príprava na testovanie deviatakov alebo prijímacie skúšky na stredné školy bola čo najľahšia. Nájdete tu napríklad zaujímavú úlohu o kupovaní anglických rožkov (V obchode bola špeciálna akcia na anglické rožky: Ak si zoberiete 4 kusy anglických rožkov, zaplatíte len za 3 rožky. Bežná cena za 1 anglický rožok je 0,39 €. Peter si zobral do košíka 22 anglických rožkov. Koľko eur za ne zaplatil?) a mnohé ďalšie.
Prehľad všetkých testov nájdete na stránke https://pohodovamatematika.sk/bonusovy-obsah-na-pohodovamatematika-sk
V obchode bola špeciálna akcia na anglické rožky: Ak si zoberiete 4 kusy anglických rožkov, zaplatíte len za 3 rožky. Bežná cena za 1 anglický rožok je 0,39 €. Peter si zobral do košíka 22 anglických rožkov. Koľko eur za ne zaplatil?
Cena za 3 rožky je 3*0,39=1,17€. Najskôr potrebujeme zistiť, koľko štvoríc sa nám zmestí do počtu 22 rožkov. Zistíme to klasickým delením so zyškom, kde zvyšok bude predstavovať počet rožkov, ktoré kúpime za bežnú cenu.
22 : 4 = 5 zv. 2
Za 5 štvoríc zaplatí 5*1,17=5,85€ a za zostávajúce 2 rožky zaplatí 2*0,39=0,78€.
Spolu teda bude platíť 5,85+0,78=6,63€
22 : 4 = 5 zv. 2
Za 5 štvoríc zaplatí 5*1,17=5,85€ a za zostávajúce 2 rožky zaplatí 2*0,39=0,78€.
Spolu teda bude platíť 5,85+0,78=6,63€
Spolu za anglické rožky zaplatí 6,63()€.
Doplňte správne číslo do rovnice, ktorej koreňom má byť číslo 7.
Za x dosadíme číslo 7 a riešime vzniknutú rovnicu s neznámou y.
3*7 – y + 2*(7-4) = 2*7 + 1
21 – y + 6 = 15 … 27 – y = 15 … 27 – 15 = y … y = 12
3*7 – y + 2*(7-4) = 2*7 + 1
21 – y + 6 = 15 … 27 – y = 15 … 27 – 15 = y … y = 12
3x – 12() + 2·[x-4] = 2x + 1
Doplňte vhodné číslo tak, aby platila rovnosť:
Najskôr potrebujeme všetky hodnoty vyjadriť v jednotkách chýbajúceho čísla. 350 l – ??? l + 12,5 l = 374,5 l. Následne už len dopočítame chýbajúcu hodnotu.
3,5 hl + 12()l + 12500 cm3 = 374,5 dm3;
Peter si v reštaurácii kúpil 6 litrov minerálky za 14,40 eur. Potom si ešte nechal naliať do pohára 3 decilitre rovnakej minerálky, ktorú vypil. Koľko eur stála minerálka v pohári?
Najskôr potrebujeme zistiť, koľko stál 1 dl minerálky. 14,40 € stojí 6 l = 60 dl, preto cena za 1 dl je 14,40 : 60 = 0,24 €. Potom už len vypočítame cenu za 3 dl … 3*0,24 = 0,72 €.
3 dl minerálky v pohári stáli 0,72() €.
Na krajskom turnaji v piškvorkách boli tímy rozdelené do 4 skupín po 3 tímy. V každej skupine hral každý s každým iba 1 zápas. Z každej skupiny následne postúpili 2 tímy (spolu 8) do playoff. Tie následne odohrali po 1 zápase, z ktorého víťaz postupoval ďalej (takto zostali 4 tímy) do semifinále. Víťazné 4 tímy v semifinále odohrali po 1 zápase, pričom porazení následne hrali ešte 1 zápas o 3. miesto a víťazi zo semifinále odohrali najdôležitejší finálový zápas o celkového víťaza. Koľko zápasov sa hralo na krajskom turnaji v piškvorkách?
Postupne počítame: Ak tímy v skupine označíme A, B, C, tak odohrané zápasy v skupine boli AB, AC, BC, teda 3. 4 skupiny po 3 zápasy je 12 zápasov. V playoff bolo 8 tímov, keďže každý tím odohral iba 1 zápas, odohrali sa v playoff celkovo 4 zápasy. V semifinále boli 4 tímy po 1 zápase, teda celkovo 2 zápasy. A ešte sa odohral 1 zápas o 3. miesto a 1zápas o 1. miesto. Spolu: 12+4+2+2=20 zápasov.
Celkovo sa na turnaji hralo 20() zápasov.
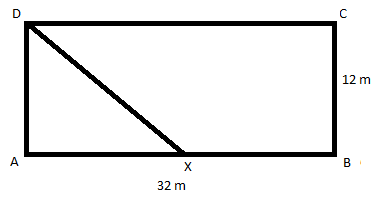
Pozemok Novákovcov mal pôvodne tvar obdĺžnika so stranami 12 m a 32 m. Susedia od nich odkúpil časť pozemku v tvare trojuholníka, ako je znázornené na obrázku. Vyznačený bod X je stredom strany AB. Koľko m pletiva potrebujú susedia Novákovcov na oplotenie svojho nového pozemku (na obr. vyznačený ako trojuholník AXD)?
Susedia Novákovcov majú pozemok tvorený pravouhlým trojuholníkom AXD. |AX|=|AB|:2=16m. |AD|=12m. Dĺžku strany XD zistíme pomocou Pytagorovej vety. XD je prepona, preto platí: |AX|2+|AD|2=|XD|2. Po dosadení: 162+122=|XD|2. A už len dopočítame XD (20m) a sčítaním všetkých 3 strán určíme množstvo pletiva v metroch, ktoré potrebujú na oplotenie.
Na oplotenie je potrebných 48() metrov pletiva.
Vo vrecúšku je vložených 12 červených loptičiek, 8 modrých loptičiek a 30 zelených loptičiek. Aká je pravdepodobnosť, že náhodne vyberieme z vrecúška modrú loptičku? Výsledok uveďte v percentách.
Pravdepodobnosť vypočítame ako podiel priaznivých možností a všetkých možností. Teda P=8/(12+8+30)=8/50=0,16=16%
Pravdepodobnosť náhodného vytiahnutia modrej loptičky je 16()%.
V tabuľke je uvedená priemerná cena za kilogram jabĺk v jednotlivých predajniach. Vypočítajte priemernú cenu za kilogram jabĺk Gala.
| predajňa | cena za kilogram jabĺk | |
| GALA | JONAGOLD | |
| 1 | 0,69 | 0,75 |
| 2 | 0,66 € | 0,84 € |
| 3 | 0,84 € | 0,72 € |
| 4 | 0,75 € | 0,92 € |
| 5 | 0,81 € | 0,88 € |
Sčítame ceny jabĺk Gala a vydelíme počtom predajní. (0,69+0,66+0,84+0,75+0,81):5=3,75:5=0,75
Priemerná cena jabĺk GALA je 0,75() € za 1 kilogram.
Súčet troch čísel je 828. Prvé číslo je o 203 menšie ako druhé. Tretie číslo je 3-krát väčšie ako prvé. Vypočítajte prvé číslo.
Ak prvé číslo je o 203 menšie ako druhé, môže povedať, že druhé číslo je teda o 203 väčšie ako prvé. Prvé číslo označíme x, spravíme jednoduchý zápis:
1. číslo … x
2. číslo … o 203 väčšie ako 1. č. … x+203
3. číslo … 3-krát väčšie ako 1. č. … 3x
spolu … 828
zostavíme rovnciu a vypočítame x: 1.č. + 2.č. + 3č. = 828
x + x + 203 + 3x = 828 … 5x + 203 = 828 … 5x = 828 – 203 … 5x = 625 … x = 625:5 = 125
1. číslo … x
2. číslo … o 203 väčšie ako 1. č. … x+203
3. číslo … 3-krát väčšie ako 1. č. … 3x
spolu … 828
zostavíme rovnciu a vypočítame x: 1.č. + 2.č. + 3č. = 828
x + x + 203 + 3x = 828 … 5x + 203 = 828 … 5x = 828 – 203 … 5x = 625 … x = 625:5 = 125
Prvé číslo je 125().
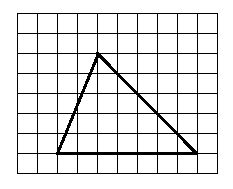
Vypočítajte obsah trojuholníka na obrázku, ak obvod malého štvorčeka je 16 cm.
Obsah trojuholníka vypočítame podľa vzťahu S = (c·vc)/2. Preto potrebujeme poznať stranu trojuholníka a výšku na ňu. Strana c je 7-násobok strany malého štvorčeka a príslušná výška je 5-násobok strany malého štvorčeka. Obvod malého štvorčeka je 16 cm, jeho strana je 16:4 = 4 cm. Potom strana c = 7*4 = 28 cm a výška vc=5*4=20cm. A už len vypočítame obsah trojuholníka.
Obsah trojuholníka je 280() cm2;
Akú dĺžku má druhá strana obdĺžnika, ak jeho obvod je 48 cm a jedna strana má dĺžku 14 cm?
Vzorec: o = 2*(a+b) Po dosadení: 48 = 2*(14+b) … vzniknutú rovnicu vyriešime.
(10 cm) (!34 cm) (!20 cm) (!32 cm)
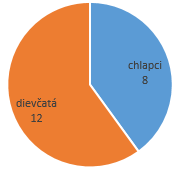
Na kruhovom diagrame je znázornený počet chlapcov a dievčat z 8. B. Koľko chlapcov pribudlo do triedy, ak sa počet dievčat nezmenil a uhol kruhového výseku znázorňujúci počet chlapcov sa zväčšil o 56°?
Najskôr zistíme, koľko stupňov pripadá na 1 žiaka pri pôvodnom počte:
8 + 12 ž. … 360°
20 ž. … 360°
1 ž. … x° = 360°:20 = 18°
8 chlapcov … 8*18°=144°.
Po novom bude počtu 8 + x chlapcov prislúchať uhol 144+56=200°, preto 12 dievčat … 160° => 1 žiak … 160:12=(40/3)°. Počet chlapcov teraz zistíme podielom 200°:(40/3)=15. Pribudlo teda 7 chlapcov.
8 + 12 ž. … 360°
20 ž. … 360°
1 ž. … x° = 360°:20 = 18°
8 chlapcov … 8*18°=144°.
Po novom bude počtu 8 + x chlapcov prislúchať uhol 144+56=200°, preto 12 dievčat … 160° => 1 žiak … 160:12=(40/3)°. Počet chlapcov teraz zistíme podielom 200°:(40/3)=15. Pribudlo teda 7 chlapcov.
(7) (!5) (!6) (!8)
Do bazéna tvaru kvádra sa zmestí 4 500 hl vody. Koľko hl vody sa do bazéna zmestí, ak jeho dĺžku zväčšíme o 20%?
Objem bazéna vypočítame podľa vzorca V = a*b*c = 4500 hl. Ak napr. stranu a zväčšíme o 20% (100%+20%=120%=1,2), dostaneme vzťah V=1,2*a*b*c. a*b*c* nahradíme číslom 4500 a následne vypočítame nový objem.
(5 400 hl) (!900 hl) (!4 520 hl) (!4590 hl)
Andrej, Milan, Dušan, Lucia a Zuzana písali písomku v náhradnom termíne. Každý z nich mal inú písomku. Ich výsledky sú uvedené v nasledujúcej tabuľke.
| Andrej | Milan | Dušan | Lucia | Zuzana | |
| dosiahnutý počet bodov | 18 | 19 | 17 | 19 | 21 |
| celkový počet bodov | 25 | 28 | 30 | 24 | 28 |
Ktorý z nich dosiahol v písomke najväčšiu percentuálnu úspešnosť?
Vypočítame percentuálnu úspešnosť jednotlivých žiakov a následne porovnáme. Napr. Andrej: 18:25=0,72=72% …
(Lucia) (!Andrej) (!Zuzana) (!Milan)
Peter a Pavol počítali príklady. Peter povedal, že výsledok príkladu (-2)3 – 23 je 0. Pavol povedal, že výsledok príkladu 23 + (-2)3 je 0. Vyberte pravdivé tvrdenie.
Každé záporné číslo umocnené na párny exponent je kladné – napr. (-3)2 = 9. Každé záporné číslo umocnené na nepárny exponent je záporné – napr. (-3)3 = -27. To by mohlo ako nápoveda stačiť :)
(Iba Pavol povedal správny výsledok.) (!Iba Peter povedal správny výsledok.) (!Obaja uviedli správny výsledok.) (!Obaja povedali nesprávny výsledok.)
Na katastrálnej mape sú zobrazené 3 pozemky, na ktorých sa nachádzajú ovocné sady. Prvý pozemok má tvar pravouhlého trojuholníka a pestujú sa na ňom jablone. Druhý pozemok je tvaru pravouhlého lichobežníka a pestujú na ňom marhule. Na treťom pozemku tvaru obdĺžnika pestujú slivky. Aká je celková rozloha týchto pozemkov v hektároch zaokrúhlená na 2 desatinné miesta?
Obsah lichobežníka vypočítať vieme. V prípade lichobežníka aj trojuholníka chýba výška, ktorú vieme dopočítať s využitím Pytagorovej vety. v2+402=502. Po vypočítaní v=30m. Celkovú rozlohu získame ako súčet rozlôh (obsahov) daných 3 pozemkov. Pravouhlý trojuholník a lichobežník spolu tvoria lichobežník, preto stačí počítať iba veľký lichobežník.
S = 150*45 + (150+85)*30/2
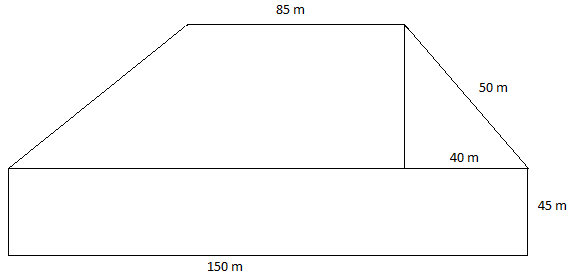
S = 150*45 + (150+85)*30/2
(1,03 ha) (!2 ha) (!0,65 ha) (!1,12 ha)
Peter vyslovil 2 tvrdenia:
A: Útvar narysovaný v pravouhlej sústave súradníc je osovo súmerný podľa osi x.
B: Útvar narysovaný v pravouhlej sústave súradníc je stredovo súmerný podľa bodu [0;1]. Posúďte pravdivosť tvrdení a vyberte správnu možnosť.
Skúste si to predstaviť: ak by sme mali útvar prehli priamo cez os x, budeme si všímať, či sa prekrýva. Ak sa prekrýva, tak je osovo súmerný podľa osi x. Tvrdenie A teda platí. Pri stredovej súmernosti so stredom v bode [0;1] ide vlastne o otočenie útvaru okolo daného bodu o 180°. Je zrejmé, že tvrdenie B neplatí.
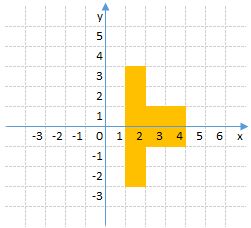
(Tvrdenie A je pravdivé a tvrdenie B je nepravdivé.) (!Tvrdenie A je nepravdivé a tvrdenie B je pravdivé.) (!Obidve tvrdenia sú nepravdivé.) (!Obidve tvrdenia sú pravdivé.)
Vypočítajte:
Najskôr vypočítajte súčin zlomkov a podiel zlomkov. Následne už len zlomky upravte na spoločný menovateľ a sčítajte.
2/3 – 2/3 – 2/5 – 2/5 = -4/5 = -0,8
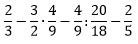
2/3 – 2/3 – 2/5 – 2/5 = -4/5 = -0,8
(-0,8) (!-2,5) (!0) (!-5)
V jednej základnej škole na Slovensku sa rozhodli zistiť, ako sú na tom ich žiaci s vedomosťami z matematiky. Výsledkom bol nasledovný graf, ktorý znázorňuje, koľkí žiaci mali na vysvedčení 1, 2, 3, 4 alebo 5.
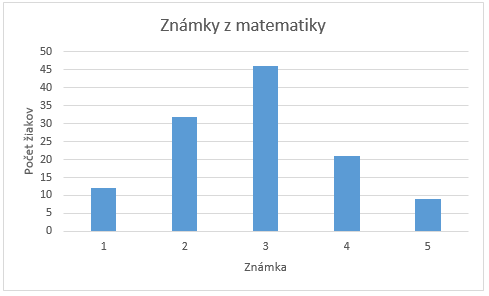
Boli vyslovené nasledovné tvrdenia:
A: Počet žiakov, ktorí mali známku 1 a počet všetkých žiakov je v pomere 1:10.
B: Priemerná známka z matematiky bola horšia ako 2,5.
Posúďte pravdivosť tvrdení a vyberte správnu možnosť.
k tvrdeniu A: jednotku mali 12 žiaci, všetkých žiakov je 120, hľadaný pomer 12:120 je po úprave na zákl. tvar 1:10
k tvrdeniu B: priemerná známka = súčet všetkých známok / počet známok = (1*12+2*32+3*46+4*21+5*9)/(12+32+46+21+9)=343/120=2,86 > 2,5
k tvrdeniu B: priemerná známka = súčet všetkých známok / počet známok = (1*12+2*32+3*46+4*21+5*9)/(12+32+46+21+9)=343/120=2,86 > 2,5
(Obidve tvrdenia sú pravdivé.
)
(!Obidve tvrdenia sú nepravdivé.
)
(!Tvrdenie A je pravdivé a tvrdenie B je nepravdivé.
)
(!Tvrdenie A je nepravdivé a tvrdenie B je pravdivé.
)
Prehľad všetkých testov nájdete na stránke https://pohodovamatematika.sk/bonusovy-obsah-na-pohodovamatematika-sk