Rovnicu tvaru ax + by + cz = d, kde a ≠ 0 alebo b ≠ 0 alebo c ≠ 0 nazývame lineárnou rovnicou s troma neznámymi x, y, z.
Trojicu čísel x0, y0, z0 nazývame riešením vyššie uvedenej rovnice, ak platí:
ax0 + by0 + cz0 = d
Rovnice tvaru
ax + by + cz = d, kde a ≠ 0 alebo b ≠ 0 alebo c ≠ 0
ex + fy + gz = h, kde e ≠ 0 alebo f ≠ 0 alebo g ≠ 0
ix + jy + kz = l, kde i ≠ 0 alebo j ≠ 0 alebo k ≠ 0
nazývame sústavou troch lineárnych rovníc s troma neznámymi x, y, z.
Trojicu čísel x0, y0, z0 nazývame riešením vyššie uvedenej sústavy rovníc, ak platí:
ax0 + by0 + cz0 = d, kde a ≠ 0 alebo b ≠ 0 alebo c ≠ 0
ex0 + fy0 + gz0 = h, kde a ≠ 0 alebo b ≠ 0 alebo c ≠ 0
ix0 + jy0 + kz0 = l, kde a ≠ 0 alebo b ≠ 0 alebo c ≠ 0
Pri riešení sústavy troch rovníc s troma neznámymi najčastejšie využívame:
- Gaussovu eliminačnú metódu;
- Cramerovo pravidlo;
- dosadzovacia metódu.
Gaussovu eliminačnú metóda:
Táto metóda spočíva v postupnej úprave sústavy rovníc na tzv. trojuholníkový tvar, kde v druhej rovnici je eliminovaná prvá neznáma a v tretej rovnici je eliminovaná prvá a druhá neznáma.
Samotný postup riešenia sústavy rovníc pomocou Gaussovej eliminačnej metódy si ukážeme na príklade.
Príklad 1:
Riešte danú sústavu rovníc s neznámymi x, y, z ∈ R:
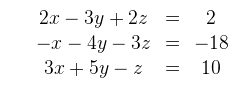
Riešenie:
Kvôli jednoduchšiemu počítaniu sa snažíme mať ako prvú rovnicu tú z troch rovníc, ktorú dokážeme najjednoduchšie upraviť na tvar s koeficientom 1 pred prvou neznámou (prípadne pred inou neznámou a vtedy by sme museli vymeniť poradie neznámych).
V našom prípade si na prvé miesto presunieme 2. rovnicu vynásobenú číslom (-1).
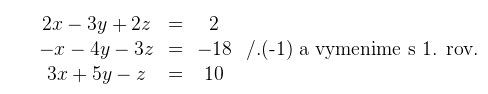
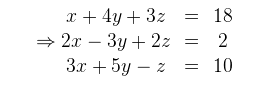
Prvú rovnicu odpíšeme.(-2)-násobok prvej rovnice pripočítame k druhej rovnici (tým eliminujeme neznámu x v druhej rovnici) a (-3)-násobok prvej rovnice pripočítame k tretej rovnici (tým eliminujeme neznámu x v tretej rovnici).
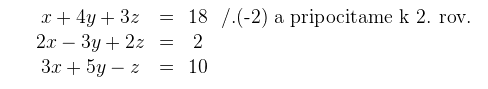
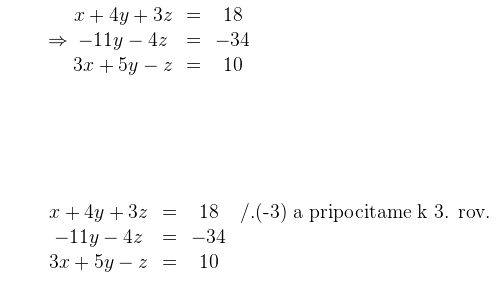
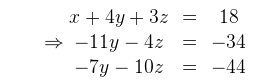
Prvú rovnicu odpíšeme. Aby sme pred neznámou y dostali v druhej a tretej rovnici navzájom opačné čísla, tak druhú rovnicu násobíme číslom (-7) a tretiu rovnicu číslom 11.

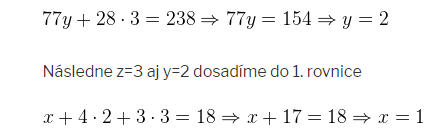
Skúšku správnosti vykonáme dosadením vypočítaných hodnôt do všetkých troch rovníc.
Riešením danej sústavy rovníc je usporiadaná trojica [x,y,z]=[1, 2, 3].
Príklad 2:
Cramerovo pravidlo:
Táto metóda umožňuje riešiť sústavu n-rovníc s n-neznámymi. Vhodnou metódou na riešenie sústav n-rovníc s n-neznámymi sa javí v prípade, ak n<4. pre n>3 je vhodnejšou metódou Gaussova eliminačná metóda. Cramerovo pravidlo predpokladá znalosť práce s maticami a determinantmi.
Príklad 3:
Riešte danú sústavu rovníc s neznámymi x, y, z ∈ R:
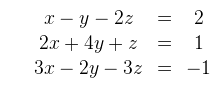
Riešenie:
Danú sústavu si zapíšeme v tvare matíc A, B:
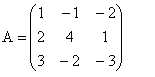
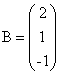
Ak determinant matice je nenulový, tak daná sústava má práve jedno riešenie. A ako určíme determinant matice A?
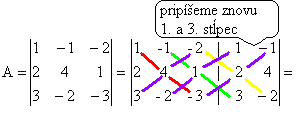
1.4.(-3) + (-1).1.3 + (-2).2.(-2) – (-2.4.3 + 1.1.(-2) + (-1).2.(-3)) = 13
Následne určíme determinanty D1, D2, D3 potrebné pre určenie neznámych. Tieto determinanty získame nahradením príslušného stĺpca determinantu stĺpcom matice B.
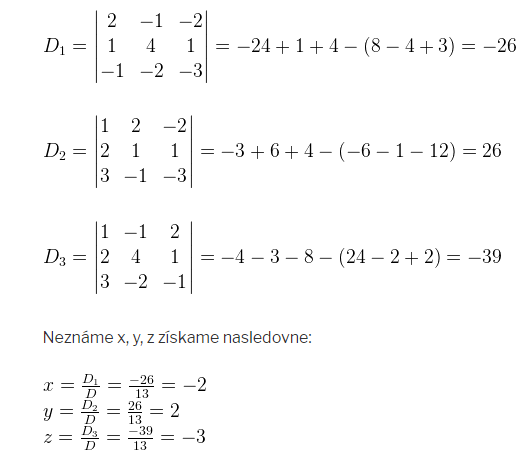
Skúšku správnosti vykonáme dosadením vypočítaných hodnôt do všetkých troch rovníc.
Riešením danej sústavy rovníc je usporiadaná trojica [x,y,z]=[-2; 2; -3].
Príklad 4:
