30. 10. 2009 | Rudolf Zrebný
↑ Hore
Neriešené príklady
Príklad 1:
Je usporiadaná dvojica [-1,3] riešením daných sústav rovníc s dvoma neznámymi?
| a) |
-3x + 2y |
= |
-9 |
b) |
5x – 2y |
= |
-11 |
c) |
-9x – 2y |
= |
3 |
|
2x + 3y |
= |
7 |
|
| d) |
2x – 3y |
= |
-11 |
e) |
-x + y |
= |
4 |
f) |
4x + 2y |
= |
2 |
|
x + y |
= |
5 |
|
x – y |
= |
4x |
|
5x – y |
= |
-8 |
|
|
2x + 3y |
= |
5 |
|
-x + 3y |
= |
10 |
Príklad 2:
Dané sústavy rovníc s dvoma neznámymi riešte v množine R x R?
| a) |
x – y |
= |
3 |
b) |
y |
= |
2x + 3 |
c) |
y |
= |
2x – 7 |
|
2x + y |
= |
9 |
|
-x + 2y |
= |
9 |
|
y |
= |
-7x + 11 |
|
| d) |
3x – 2y |
= |
1 |
e) |
x – 7y |
= |
-3 |
f) |
5x + 3y |
= |
-2 |
|
2x – 3y |
= |
4 |
|
-3x + 5y |
= |
-7 |
|
-2x – 7y |
= |
-5 |
|
| g) |
2x – 3y |
= |
-5 |
h) |
x – 2y |
= |
1 |
|
|
-4x + 6y |
= |
9 |
|
3x – 6y |
= |
3 |
|
Príklad 3:
Dané sústavy rovníc s dvoma neznámymi riešte v množine Z x N?
| a) |
x + y |
= |
1 |
b) |
2x – y |
= |
4 |
|
x – y |
= |
-3 |
|
3x + 4y |
= |
-5 |
|
| c) |
2x + y |
= |
3 |
d) |
4 – 3x |
= |
7y |
|
x – 3y |
= |
-2 |
|
2y – 3x |
= |
5 |
Príklad 4:
Určte konštantu c ak viete, že usporiadaná dvojica [x,y]=[-2,b] je jediným riešením danej sústavy rovníc.
| a) |
x – 3y |
= |
c |
b) |
(5x – 2y)·c |
= |
64 |
|
-xc + 2y |
= |
8 |
|
x – 3y +9 |
= |
–c |
Príklad 5:
Dané sústavy rovníc riešte v množine N x N.
| a) |
2y + x |
= |
18 |
b) |
y + x |
= |
-2 |
|
y – 5 |
= |
-2 |
|
2x + 3y |
= |
-7 |
Príklad 6:
Dané sústavy rovníc riešte v množine M = (-∞,-3> x (-7,∞).
| a) |
3·(2x – 3y) – 5x |
= |
-[-(2x + y)·2 – 3] + 9 |
|
-2·(x – 2y) + y |
= |
3·(x – 5y) + 20 |
|
| b) |
(x – y)2 – (3x – 2y)(3x + 2y) |
= |
-5x – 8x2 + 5y2 |
|
x – y |
= |
-(2x + y) |
Príklad 7:
Nájdite riešenie daných sústav rovníc ak [x,y] ∈ Z x R.
| a) |
x – 2y |
= |
–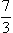 |
b) |
2x – 5y |
= |
-4 |
c) |
2x – 5 |
= |
-3y – 1 |
|
2x + 3y |
= |
0 |
|
x + y |
= |
1.5 |
|
5x + 1 |
= |
y – 6 |
Príklad 8:
Určte lineárnu funkciu f: y = ax + b, ktorej graf prechádza bodmi:
| a) [-1,2], [1,2] |
|
b) [-1,2], [1,4] |
| c) [2,3], [-3,8] |
|
d) [0.5,-3.5], [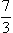 ,2] ,2] |
Príklad 9:
Riešte danú sústavu rovníc v množine R x R.
Pomôcka: využite substitúciu 1/x = a, 1/y = b
|
2 |
– |
3 |
= |
2 |
|
| x |
y |
| – |
1 |
+ |
5 |
= – |
23 |
| 2x |
y |
12 |
Príklad 10:
Riešte danú sústavu rovníc v množine N x N.
Pomôcka: využite substitúciu 1/(x-2) = a, 1/(y+3) = b
| 2 |
– |
4 |
= – |
1 |
| 3·(x – 2) |
y + 3 |
3 |
- a) nie; b) áno; c) áno; d) nie; e) nie; f) áno
- a) [4; 1]; b) [1; 5] c) [2; -3]; d) [-1; -2]; e) [4; 1]; f) [-1; 1]; g) nemá rieš. h) [x; y] = [t; 0,5t-0,5]; t∈R
- a) [-1; 2]; b) nemá riešenie, lebo y=-2 ∉ N; c) [1;1]; d) [-1; 1]
- a) c = 7; b) c1=-6; c2=-16;
- a) [2; 8]; b) nemá riešenie, lebo y=-3 ∉ N
- a) [-4; 0]; b) [0; t]; t ∈ (-7,∞)
- a) [-1; 2/3]; b) nemá riešenie, lebo x=0,5 ∉ Z; c) [-1; 2];
- a) y = 2; b) y = x + 3; c) y = -x + 5; d) y = 3x – 5
- [2; -3]
- [3; 1]
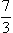
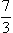 ,2]
,2]