Nech f a g sú lineárne funkcie, ktorých definičné obory D(f) a D(g) a obory hodnôt sú H(f) a H(g) sú podmnožinami množiny reálnych čísel. Potom výrokovu formu
f(x) = g(x),
ktorá každému číslu x0∈D(f)∩D(g) priradí výrok f(x0) = g(x0), nazývame rovnica s jednou neznámou.
Rovnica je teda výroková forma, preto obsahuje aspoň jednu neznámu, ale rovnosť je výrok.
Napr. x2+2x=3x2-5x je rovnica, ale (-2)2+2(-2)=3(-2)2-5(-2) je rovnosť.
Ak uvažujeme o rovnici tvaru
f(x) = g(x),
tak výrazu f(x) hovoríme ľavá strana rovnice
a výrazu g(x) pravá strana rovnice.
Často sa môžeme vo všeobecnosti stretnúť i so zápisom L(x) = P(x).
Hodnoty neznámej xk, pre ktoré platí rovnosť L(xk)=P(xk) sa nazývajú korene (riešenia) rovnice.
Oborom riešenia rovnice nazývame množinu M, v ktorej hľadáme korene rovnice.
Definičným oborom rovnice nazývame podmnožinu množiny M, v ktorej sú definované obidva výrazy L(x), P(x) alebo prienik definičných oborov týchto výrazov. Označujeme ho D.
Množinu všetkých koreňov (riešení) rovnice označujeme K. Niekedy sa stretnete aj s označením P.
Platí: K ⊂ D ⊂ M
Príklad 1:
Riešte rovnicu 5x + 7 = 3 s neznámou x ∈ R.
Riešenie:
Obor riešenia M = R; definičný obor D = R; táto rovnica má v obore D práve jeden koreň x = –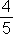
alebo zapíšeme K = {-}.
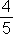Ak by sme uvažovali obor riešenia M = Z; definičný obor D = Z; táto rovnica by v definičnom obore D nemala riešenie.
Príklad 2:
Riešte rovnicu x-1 = 2 s neznámou x∈R.
Riešenie:
Obor riešenia M = R; definičný obor D = <1;∞); táto rovnica má v obore D práve jeden koreň x = 5 alebo zapíšeme K = {5}.