Lineárna nerovnica s neznámou x ∈ R je každá nerovnica tvaru ax + b < 0, ax + b ≤ 0, ax + b > 0, ax + b ≥ 0, kde a, b sú ľubovoľné reálne čísla.
Riešenie lineárnej nerovnice:
Nerovnicu upravíme tak, že odčítame b od oboch strán nerovnice, čím ju upravíme na tvar ax < -b, ax ≤ -b, ax > -b, ax ≥ -b. Pri riešení môžu potom nastať tri prípady:
Ak a < 0, potom z nerovnosti ax < -b dostaneme x > – 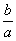
resp. z nerovnosti ax > -b dostaneme x < – 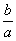 ;
;
Napr.
z -2x < -1 dostaneme x > 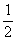
z -5x < 3 dostaneme x > – 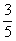
z -7x > -5 dostaneme x < 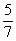
z -3x > 8 dostaneme x < – 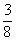
Ak a > 0, potom z nerovnosti ax > -b dostaneme x > – 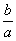
resp. z nerovnosti ax < -b dostaneme x < – 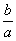 ;
;
Napr.
z 5x < -3 dostaneme x < – 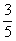
z 2x < 1 dostaneme x < 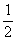
z 7x > 5 dostaneme x > 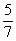
z 3x > -8 dostaneme x > – 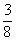
Ak a 0 potom 0·x < –b alebo 0·x > –b . Táto nerovnica je splnená buď pre všetky x ∈ R alebo pre žiadne x ∈ R.
Ekvivalentné úpravy nerovníc:
- vzájomná výmena strán nerovnice so súčasnou zmenou znaku nerovnosti na obrátený;
- nahradenie ľubovoľnej strany nerovnice výrazom, ktorý sa jej rovná v celom obore riešenia nerovnice, pričom znak nerovnosti sa nezmení;
- pripočítaním toho istého čísla alebo výrazu s neznámou, ktorý je definovaný v celom obore riešenia, k obom stranám nerovnice, pričom znak nerovnosti sa nemení;
- vynásobenie oboch strán nerovnice kladným číslom alebo výrazom s neznámou, pričom znak nerovnosti sa nemení;
- vynásobenie oboch strán nerovnice záporným číslom nebo výrazom s neznámou, pritom znak nerovnosti sa zmení v obrátený;
- umocnenie oboch strán nerovnice prirodzeným mocniteľom, ak sú obe strany nerovnice nezáporné, pritom znak nerovnosti sa nemení;
- odmocnenie oboch strán nerovnice prirodzeným odmocniteľom, ak sú obe strany nerovnice nezáporné, pričom znak nerovnosti sa nemení;
- zlogaritmovaní oboch strán nerovnice pri tom istom základe väčšom ako 1, ak sú obe strany nerovnice kladné, pritom znak nerovnosti sa nemení.
Príklad 1:
Riešte nerovnicu 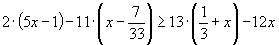 s neznámou x ∈ R.
s neznámou x ∈ R.
Riešenie:
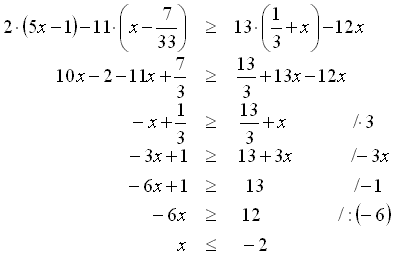
Teda množina riešení danej nerovnice je P = (-∞; -2>.
