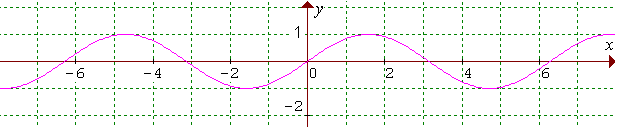
Funkciu f nazývame periodická funkcia práve vtedy, keď existuje také reálne číslo p≠0, že pre každé x ∈ D(f) je aj x ± p ∈ D(f) a platí:
f(x ± p) = f(x)
Číslo p nazývame perióda funkcie f.
Vo fyzike sa perióda označuje T.
Ak má daná funkcia f periódu p, ľahko dokážeme, že pre každé celé číslo k platí: f(x + kp) = f(x).
Teda daná funkcia má i periódu kp.
Dôkaz:
V(k): f(x + kp) = f(x)
1. Predpokladáme, že pre k = 1 platí V(1): f(x ± p) = f(x)
2. Dokážeme platnosť implikácie V(k) ⇒ V(k+1):
V(k): f(x + kp) = f(x) … indukčný predpoklad
V(k+1): f(x + (k+1)p) = f(x + p + kp) = f(x + kp) = f(x)
Takže implikácia V(k) ⇒ V(k+1) je pravdivý výrok, preto platí:
Ak má funkcia f periódu p, potom má aj periódu kp, kde k∈Z.
Graf periodickej funkcie sa pravidelne opakuje po intervaloch, ktorých dĺžka je rovná základnej perióde p.
Ukážky periodických funkcií:
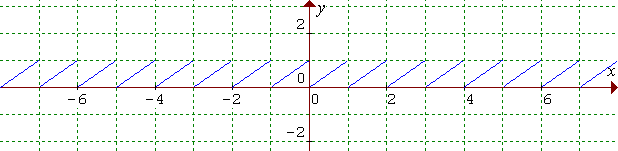
f: y = x – [x], D(f) = R
Pre tých, ktorí nevedia, čo znamená [x], tak …
Pre každé reálne číslo x, existuje celé číslo z, pre ktoré platí:
z ≤ x < z+1
Celé číslo z, pre ktoré platí vyššie uvedené nazývame dolná celá časť (alebo len celá časť) a označujeme ho [x].
Napr. [3,56] = 3
Graf funkcie f: y = x – [x], D(f) = R
Významnými periodickými funkciami sú goniometrické funkcie.
Napr. g: y = sinx, D(g) = R