Obsah článku:
Vypočítať obvod a obsah obdĺžnika v prípade známych strán nie je problémom zrejme pre nikoho z vás. Stačí využiť známe vzorce:
Obvod obdĺžnika: o = 2a + 2b
Obsah obdĺžnika: S = a ⋅ b
V tomto článku sa budeme venovať rôznym slovným úlohám vedúcim k riešeniu obsahu alebo obvodu obdĺžnika.
Pozemky
Peter vlastní pozemok v tvare obdĺžnika s rozmermi 200 m a 150 m. Jeho sused Ondrej je majiteľom pozemku v tvare obdĺžnika s rovnakou výmerou a dĺžkou 250 m. Vypočítajte šírku Ondrejovho pozemku.
Riešenie:
Výmery (obsahy) oboch pozemkov sú rovnaké. Keďže rozmery Petrovho pozemku poznáme, môžeme si vypočítať výmeru pozemku.
a = 200 m
b = 150 m
S = a ⋅ b = 200 ⋅ 150 = 30 000 m²
Výmera Ondrejovho pozemku je rovnaká, preto:
S = 30 000 m²
a = 250 m
b = ?
S = a ⋅ b
30000 = 250 ⋅ b
b = 30000 : 250 = 120 m
Šírka Ondrejovho pozemku je 120 metrov
Jednoduché príklady na obsah a obvod obdĺžnika
1. Obdĺžnik má dĺžku strany 8 cm a šírku strany 5 cm. Vypočítajte jeho obsah a obvod.
Riešenie:
dĺžka … a = 8 cm
šírka … b = 5 cm
o = ? cm
S = ? cm²
o = 2(a + b) = 2(8 cm + 5 cm) = 26 cm
S = a x b = 8 cm x 5 cm = 40 cm²
2. Obdĺžnik má dĺžku strany 12 cm a jeho obvod je 46 cm. Vypočítajte šírku a obsah obdĺžnika.
Riešenie:
dĺžka … a = 12 cm
obvod … o = 46 cm
šírka … b = ? cm
obsah … S = ? cm²
o = 2(a + b)
46 cm = 2(a + b) /:2
23 cm = a + b
23 cm = 12 cm + b /-12 cm
11 cm = b
S = a x b = 12 cm x 11 cm = 132 cm²
3. Obdĺžnik má obvod 56 cm a jeho šírka je 8 cm. Vypočítajte dĺžku a obsah obdĺžnika.
Riešenie:
o = 56 cm
b = 8 cm
a = ? cm
S = ? cm²
o = 2(a + b)
56 = 2(a + b) /:2
28 = a + 8 /-8
20 cm = a
S = a x b = 20 cm x 8 cm = 160 cm²
4. Obdĺžnik má obvod 72 cm a jeho dĺžka je dvojnásobok jeho šírky. Vypočítajte dĺžku a obsah.
Riešenie:
o = 72 cm
dĺžka je 2-násobok šírky
a = ? cm
S = ? cm²
Ak označíme šírku b obdĺžnika ako x, potom dĺžka a = 2x
o = 2(a + b)
72 cm = 2(2x + x)
72 cm = 4x + 2x
72 cm = 6x /:6
12 cm = x ….. šírka obdĺžnika b = 12 cm
Dĺžka a = 2x = 24 cm
S = a x b = 24 cm x 12 cm = 288 cm²
5. Obdĺžnik má obsah 64 cm² a jeho dĺžka je 16 cm. Vypočítajte šírku a obvod.
S = 64 cm²
a = 16 cm
b = ? cm
o = ? cm
Pre výpočet šírky b dosadíme známe hodnoty do vzorca S = a * b a dostaneme:
S = a*b
64 = 16*b /:16
4 cm = b
Obvod obdĺžnika je o = 2a + 2b. Dosadením známych hodnôt dostaneme:
o = 2 * 16 cm + 2 * 4 cm = 32 cm + 8 cm = 40 cm
Takže šírka obdĺžnika je 4 cm a obvod je 40 cm.
6. Obdĺžnik má obsah 45 cm² a jeho šírka je 5 cm. Vypočítajte dĺžku a obvod.
S = 45 cm²
b = 5 cm
a = ? cm
o = ? cm
Pre výpočet dĺžky a dosadíme do vzorca S = a * b známe hodnoty.
S = a*b
45 = a*5 /:5
9 = a ……. a = 9 cm
o = 2 * 9 cm + 2 * 5 cm = 18 cm + 10 cm = 28 cm
Dĺžka obdĺžnika je 9 cm a obvod je 28 cm.
Slovné úlohy na obsah a obvod obdĺžnika
1. Poľnohospodár na pozemku s výmerou 15 000 m² vysial jačmeň. Na inom pozemku s rovnakou výmerou, ale dĺžkou 300 metrov sa rozhodol pestovať kukuricu. Akú šírku má pozemok s kukuricou?
Riešenie:
Aby sme zistili šírku pozemku s kukuricou, musíme najprv zistiť jeho plochu.
Vieme, že má rovnakú výmeru ako pozemok s jačmeňom, teda 15 000 m². Plocha obdĺžnika sa vypočíta ako súčin jeho dĺžky a šírky, teda:
plocha = dĺžka x šírka ……. S = a x b
Pretože vieme dĺžku pozemku s kukuricou (b = 300 metrov) a jeho plochu (S = 15 000 m²), môžeme vypočítať jeho šírku:
S = a x b
15 000 m² = 300 m x b
b = 15 000 m² : 300 m
b = 50 metrov
Pozemok s kukuricou má šírku 50 metrov.
Na pozemku tvaru obdĺžnika s výmerou 32 m² chceme postaviť plot. Dĺžka jednej strany pozemku je dvojnásobkom dĺžky kratšej strany pozemku. Koľko pletiva potrebujeme na oplotenie pozemku, ak budeme mať dve proti sebe umiestnené 2 bránky široké 2 m?
Riešenie:
Najskôr potrebujeme zistiť strany obdĺžnika (záhrady).
výmera = obsah …. 32 m²
kratšia strana … b = x m
dlhšia strana … dvojnásobok kratšej strany … a = 2 · b = 2x
S = a · b
32 = x · 2x
32 = 2x²>2
16 = x² /√
4 = x ….. b = 4 m …. a = 2x = 8 m
Aby sme zistili potrebnú dĺžku pletiva, tak potrebujeme vypočítať obvod obdĺžnika so stranami 4 m a 8 m.
o = 2 · (a + b) = 2 · (4 + 8) = 2 · 12 = 24 m
Nesmieme zabudnúť na odpočítanie šírky bránok.
dĺžka pletiva = o – 2 · 2 = 24 – 4 = 20 m
Na oplotenie pozemku budeme potrebovať 20 metrov pletiva.
Pôdorys obytnej budovy má tvar obdĺžnika s obvodom 50 m. Aká je jej dĺžka, ak šírka je 8 m?
Riešenie:
o = 50 m
b = 8 m
a = ? m
o = 2a + 2b
50 = 2a + 2·8
50 = 2a + 16 /-16
34 = 2a /:2
17 m = a
Dĺžka obytnej budovy je 17 metrov.
Máme koberček v tvare obdĺžnika s dĺžkou 3 m a šírkou 2 m. Potrebujeme ho obšiť po celom obvode. Aká bude dĺžka obšitia?
Riešenie:
Dĺžka obšitia predstavuje obvod daného obdĺžnika.
o = 2 · (3 + 2) = 2 · 5 = 10 m
Dĺžka obšitia koberčeka bude 10 m-
Peter chce postaviť drevený plot okolo svojho dvora. Dvor má dĺžku 15 metrov a šírku 10 metrov. Koľko metrov štvorcových drevených dosiek potrebuje na postavenie plotu s výškou 2 metre? Dosky sú tesne vedľa seba bez medzier.
Riešenie:
Najskôr je potrebné vypočítať obvod obdĺžnika (plot).
o = 2 · (15 + 10) = 2 · 25 = 50 m
Dĺžka plotu je 50 metrov. Ak má byť plot vysoký 2 metre, tak množstvo dosiek vypočítame jednoducho ako obsah obdĺžnika so stranami 50 m a 2 m.
S = a · b = 50 · 2 = 100 m²
Na postavenie plota potrebuje Peter 100 m˛ dosiek.
Mária potrebuje pokryť celú podlahu miestnosti obdĺžnikovými dlaždicami. Rozhodla sa použiť dlaždice, ktorých rozmer je 40 cm x 60 cm. Ak má miestnosť dĺžku 5,2 m a šírku 4,2 m, najmenej koľko dlaždíc potrebuje?
Riešenie:
Potrebujeme docieliť, aby bol pri pokrývaní podlahy čo najmenší odpad. Preveríme teda, čí čísla reprezentujúce rozmery miestnosti sú deliteľné číslami reprezentujúcimi rozmery dlaždíc.
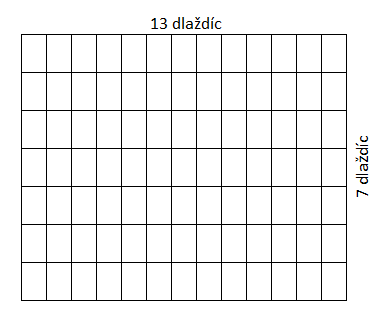
5,2 m = 520 cm ….. 520 : 40 = 13
4,2 m = 420 cm ….. 420 : 60 = 7
Z uvedeného vyplýva, že na dĺžku miestnosti sa zmestí 13 dlaždíc a na šírku 7. Aby sme zistili počet dlaždíc, ktoré potrebujeme, stačí vypočítať súčin 13 · 7 = 91
Mária potrebuje najmenej 91 dlaždíc.
Potrebujete pomôcť? Napíšte mi!