Obsah článku:
Už pred rokom 3000 p.n.l. vedeli Egypťania zapisovať čísla pomocou hieroglyfov. Toto obdobie je zároveň obdobím, kedy boli postavené pyramídy. Napríklad Veľká pyramída v Gize bola postavená okolo roku 2650 p.n.l. a je dôkazom veľmi vysokej úrovne vzdelanosti a tiež pozoruhodných inžinierskych schopností Egypťanov na danú dobu.
Hieroglyfické číslovky možno nájsť na rôznych artefaktoch, kamenných vázach, chrámoch, …, ale tieto číslovky neposkytujú žiaden konkrétny obraz o počítaní a narábaní s nimi. Pravdepodobne to bolo spôsobené aj tým, že tieto číslovky boli vytesávané do kameňa, čo značne spomaľovalo ich zapisovanie.
Značný pokrok v zapisovaní a narábaní s číslami prinieslo so sebou obdobie, kedy sa v Egypte začal používať na písanie papyrus. Vzhľadom na nestálosť tohto materiálu sa zachovali len dva dokumenty a to Rhindov papyrus a Moskovský papyrus.
Rhindov papyrus je pomenovaný podľa škótskeho egyptológa Henryho Rhinda, ktorý tento papyrus kúpil v luxore v r. 1858. Obsahuje 87 matrematických problémov, ktoré na papyrus zapísal okolo r. 1650 p.n.l. pisár Ahmes, ktorý vyhlásil, že je kópiou o dvesto rokov staršieho dokumentu. V súčasnosti sa nachádza v expozícii Britského múzea.

Moskovský papyrus v r. 1947 získal ruský vedec V. S. Golenišev, preto tento papyrus dnes nájdeme v Moskovskom múzeu. Obsahuje menej úloh ako Rhindov papyrus – 25. Jeho pôvod je datovaný podobne ako Rhindov papyrus približne do r. 1700 p.n.l. Jeho dĺžka je takmer 97 cm.

Prínosy egyptskej matematiky:
- prvý symbol pre čísla;
- zaviedli desiatkový systém pre čísla, váhy a merania;
- rozvinuli techniky pre delenie a násobenie prirodzených čísel a zlomkov;
- zaviedli spôsoby výpočtov obsahov obdĺžnikov, kruhov, trojuholníkov a objemy kvádrov, zrezaných kužeľov a pyramíd.
Pravdepodobne budete so mnou súhlasiť, že by bolo smiešne pýtať sa vás, čo je to čitateľ, menovateľ, 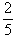 , …
, …
Určite uznáte, že pre vás sú tie pojmy samozrejmosťou a predstavte si, že Egypťania tieto pojmy vôbec nepoznali. Pýtate sa, ako zapisovali teda zlomky? Používali znaky iba pre zlomky jedna polovica, jedna tretina, jedna štvrtina, jedna pätina, atď. Zapisovali ich tak, že nad číslo v menovateli dávali znak, ktorý mal tvar oka.
Zlomky, ktoré my zapíšeme ako 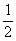 ,
, 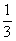 ,
, 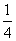 ,
, 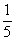 ,
, 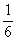 , … zapisovali v Egypte takto:
, … zapisovali v Egypte takto: 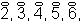 , …
, …
A bežné čísla?
- Číslo 1 zapísali jednoduchou čiarou – |;
- číslo 10 zobrazovali v tvare podkovy – ∩
- číslo 100 zapisovali v tvare
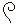
- číslo 1 000 zapisovali v tvare
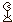
- číslo 10 000 zapisovali v tvare
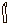
- číslo 100 000 zapisovali v tvare
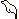
- číslo 1 000 000 zapisovali v tvare
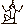
Napr. číslo 127 napísali nasledovne: 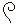 ∩∩
∩∩
Sčítanie a odčítanie nebolo pre starých Egypťanov samozrejme problémom. A ako sa vysporiadali s násobením a delením?
Pri násobení a delení využívali metódy zdvojnásobenia a polenia alebo tiež používali násobky desiatich alebo piatich.
Na Rhindovom papyruse na nachádza napr. úloha, kde treba vynásobiť čísla 41 a 59. Postupuje sa nasledovne: Zapíšeme si číslo 1 do ľavého a číslo 59 do pravého stĺpca. Postupne zapisujeme dvojnásobky čísel v ľavom a pravom stĺpci ta, aby sme v ľavom stĺpci neprekročili číslo 41. Keď sa pozriete nižšie, určite ste zistili, že napr. 4 236 znamená, že 4-násobkom čísla 59 je číslo 236. Tak poďme na to.
41 59
| 1 | 59 |
| 2 | 118 |
| 4 | 236 |
| 8 | 472 |
| 16 | 944 |
| 32 | 1888 |
Keďže 41 je menšie ako 64, tak nepotrebujeme pokračovať nad rámec 32. Teraz sa pozrieme na rad čísel, ktoré sme dostali. Využívame ľavý stĺpec. Vidíme, že 41-32=9, 9-8=1, 1-1=0, preto sčítame príslušné čísla z právého stĺpca teda 32-násobok, 8-násobok a 1-násobok …
1888 + 472 + 59 = 2419
Teda súčinom čísel 41 a 59 je číslo 2419.
Môžte si vyskúšať vypočítať nejaké príklady a uvidíte, či sa vám to podarí.
Ako sme už spomínali, pri delení používali egypťania podobnú metódu. Poďme sa spolu pozrieť, ako napr. delili číslo 1470 číslom 42.
| 1 | 42 |
| 2 | 84 |
| 4 | 168 |
| 8 | 336 |
| 16 | 672 |
| 32 | 1344 |
Ďalej nepokračujeme, lebo 64×42 by vysoko prevyšovalo číslo 1470. A aký bude výsledok?
1470 – 1344 = 126, 126 = 84 + 42, čiže výsledok dostaneme sčítaním príslušných čísel v ľavom stĺpci.
32 + 2 + 1 = 35
Podielom čísel 1470 a 42 je číslo 35.
Pýtate sa, čo v prípade, ak nevychádza celočíselný podiel?
Pozrime sa, ako sa s tým vysporiadali v starovekom Egypte.
Úloha: Určte podiel čísel 2350 a 27.
| 1 | 27 |
| 2 | 54 |
| 4 | 108 |
| 8 | 216 |
| 16 | 432 |
| 32 | 864 |
| 64 | 1728 |
Opäť ďalej nepokračujeme, lebo 128-násobok čísla 27 by vysoko prevýšil číslo 2350.
2350 – 1728 = 622, 622 – 432 = 190, 190 – 108 = 82, 82 – 54 = 28, 28 – 27 = 1, ďalej nemáme odčítať aký násobok, preto sčítame tie čísla, ktoré môžme a zvyšok využijeme na zápis zlomku.
64 + 16 + 4 + 2 + 1 = 87
Teda podiel čísel 2350 a 27 je číslo 87 a zlomok 1/27.
