Korene kvadratickej rovnice a graf kvadratickej funkcie
Pravdepodobne ste si uvedomili, že pri načrtávaní grafu alebo určovaní vlastností kvadratickej funkcie sme zostávali (na Pohodovej matematike) pri určovaní priesečníka grafu kvadratickej funkcie s osou y, ale na priesečníky s osou x sme „akosi zabúdali“.
A dôvod?
Prozaický, pri určovaní priesečníkov paraboly so súradnicovou osou y potrebujeme vedieť riešiť kvadratickú rovnicu. Veď posúďte sami.
Daná je kvadratická funkcia f: y = ax2 + bx + c, kde a≠0.
Vieme, že priesečník grafu tejto funkcie s osou x má súradnice Px=[x,0], teda poznáme y-ovú súradnicu priesečníka.
Dosaďme ju do predpisu kvadratickej funkcie.
0 = ax2 + bx + c
Usmievate sa? Vidíte dobre – dostali sme kvadratickú rovnicu, ktorej vyriešením získame x-ovú súradnicu priesečníka grafu danej kvadratickej funkcie so súradnicovou osou x.
Príklad 1:
Určte priesečníky Px grafu kvadratickej funkcie na obrázku so súradnicovou osou x.
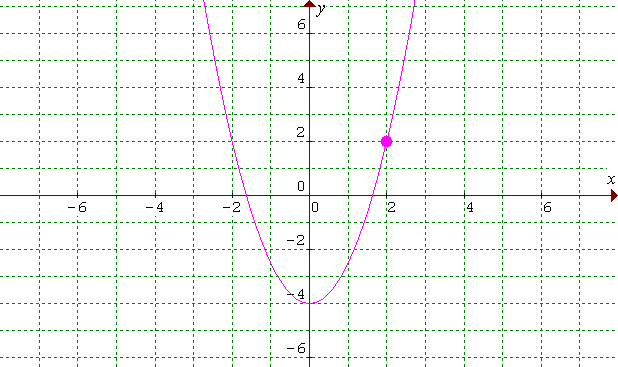
Riešenie:
Aby sme mohli určiť Px, potrebujeme poznať predpis kvadratickej funkcie, ktorej graf je na obrázku.
f: y = ax2 + bx + c
Z grafu vieme vyčítať: V=[0, -4], Py=[0,-4], bod [2,2]
Keďže Py=[0,-4], tak c = -4, teda f: y = ax2 + bx – 4
Keďže V=[0,-4], tak b = -4, keďže 0=-b/2a (bližšie pozri Kvadratická funkcia), teda f: y = ax2 – 4
Keďže poznáme bod [2, 2], tak jeho súradnice dosadíme do upraveného predpisu kvadratickej funkcie
y = ax2 – 4
2 = a·22 – 4 /+4
6 = 4a /:4
a = 1,5
Poznáme teda predpis kvadratickej funkcie, ktorej graf je na obrázku:
f: y = 1,5x2 – 4
Px=[x, 0]
Dosadením do predpisu funkcie dostaneme: 0 = 1,5x2 – 4
Vyriešime danú kvadratickú rovnicu a získame jej korene: x1,2=± 2·2/3.
Px1 = [2·2/3, 0], Px2 = [-2·2/3, 0],
