Obsah článku:
- 1. Ktoré z daných funkcií sú párne alebo nepárne?
- 2. Rozhodnite, na ktorých obrázkoch sú grafy párnych alebo nepárnych funkcií:
- 3. Doplňte nasledovné obrázky tak, aby predstavovali grafy párnych funkcií:
- 4. Doplňte nasledovné obrázky tak, aby predstavovali grafy nepárnych funkcií:
- 5. Dokážte, že funkcia f: y = 2x – 1 je rastúca.
- 6. Ktoré z funkcií na obrázkoch sú prosté, určte ich extrémy:
- 7. Ktoré z daných funkcií sú zhora (zdola) ohraničené?
- 8. Určte intervaly, na ktorých sú dané funkcie rastúce.
- 9. Určte z grafu funkcie f jej D(f) a H(f), monotónnosť, extrémy, paritu, ohraničenosť, priesečníky so súradnicovými osami.
↑ Hore
1. Ktoré z daných funkcií sú párne alebo nepárne?
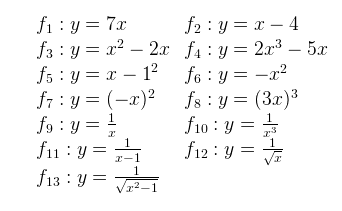
2. Rozhodnite, na ktorých obrázkoch sú grafy párnych alebo nepárnych funkcií:
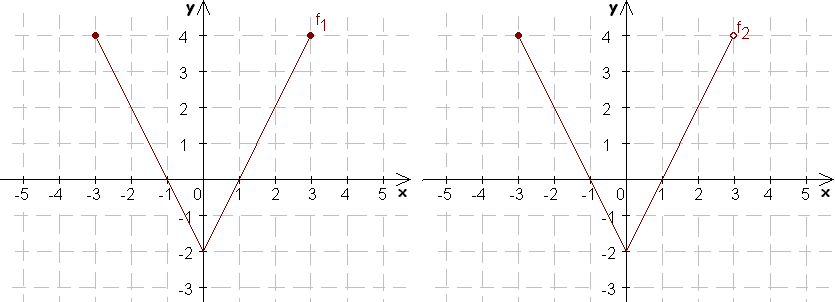
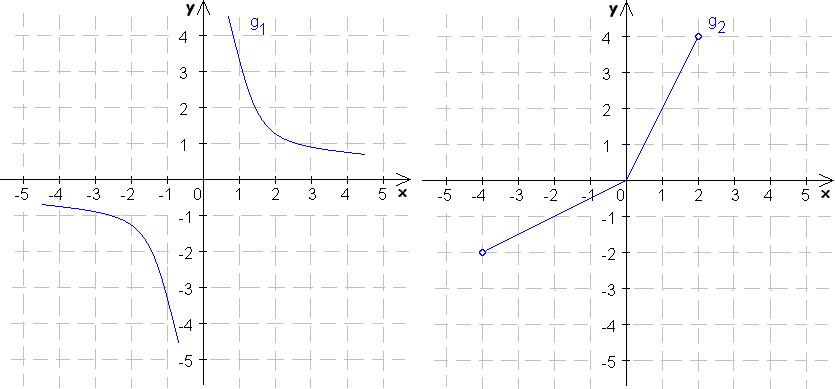
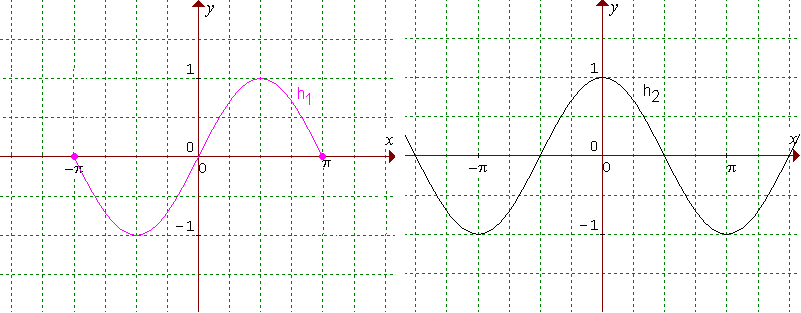
3. Doplňte nasledovné obrázky tak, aby predstavovali grafy párnych funkcií:
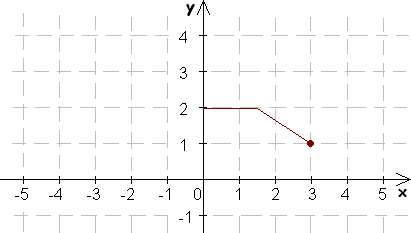
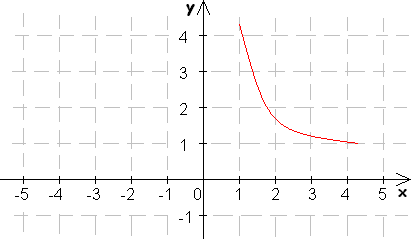
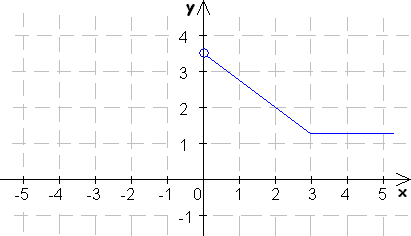
4. Doplňte nasledovné obrázky tak, aby predstavovali grafy nepárnych funkcií:



5. Dokážte, že funkcia f: y = 2x – 1 je rastúca.
6. Ktoré z funkcií na obrázkoch sú prosté, určte ich extrémy:
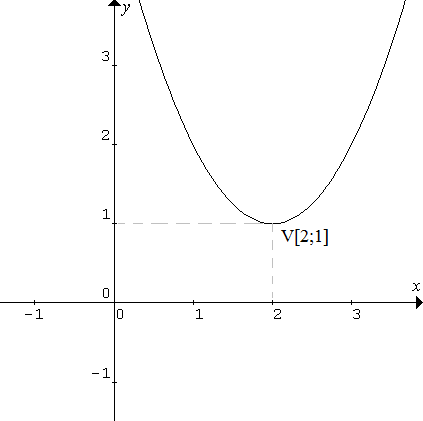
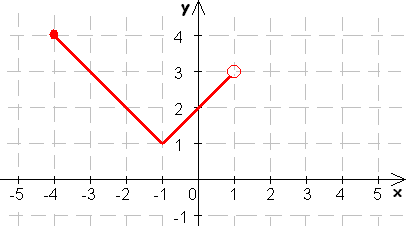
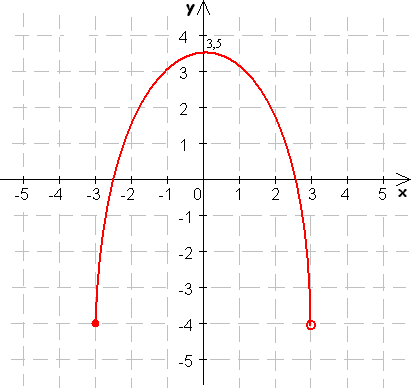
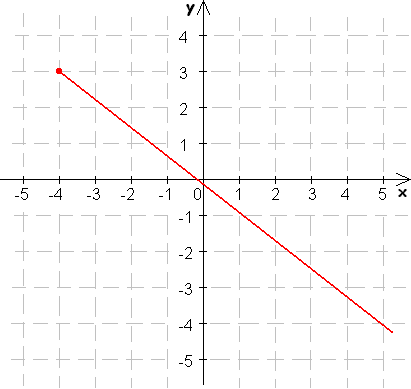
7. Ktoré z daných funkcií sú zhora (zdola) ohraničené?
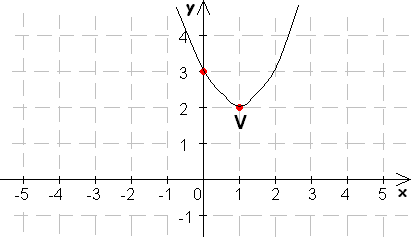
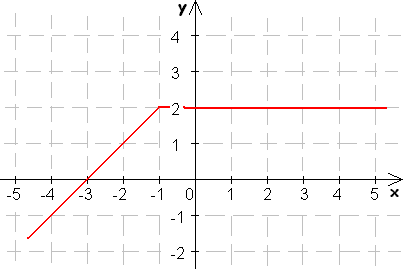

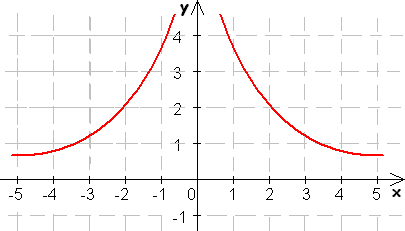
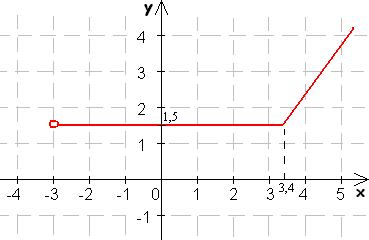
8. Určte intervaly, na ktorých sú dané funkcie rastúce.

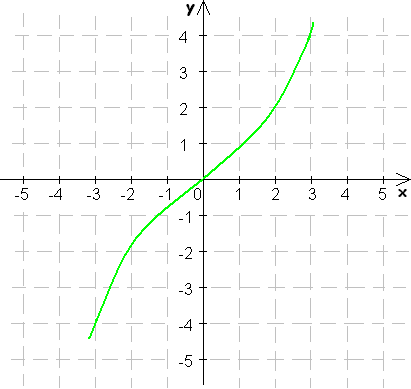
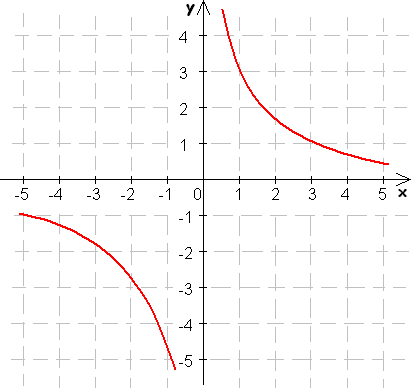
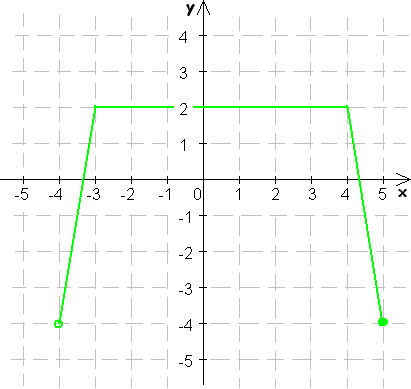

9. Určte z grafu funkcie f jej D(f) a H(f), monotónnosť, extrémy, paritu, ohraničenosť, priesečníky so súradnicovými osami.

