Kvadratickou funkciou nazývame každú funkciu
f: y = ax2 + bx + c, kde a≠0, a, b, c ∈ R
Ak by sme použili koeficienty a = 1, b = c = 0, tak by sme dostali kvadratickú funkciu
f: y = x2,
ktorá je často nazývaná základná kvadratická funkcia. Neskôr sa k tejto funkcii ešte vrátime.
Skôr ako sa pustíme do riešenia konrétnych zadaní, spravíme si malé predstavenie kvadratickej funkcie – jej grafu a vlastností.
Graf kvadratickej funkcie:
Grafom každej kvadratickej funkcie je krivka, ktorú nazývame parabola. Parabola je súmerná podľa osi o rovnobežne so súradnicovou osou y. Jej tvar vidíte nižšie na obrázku.
Graf kvadratickej funkcie f: y = x2 – 4x + 5
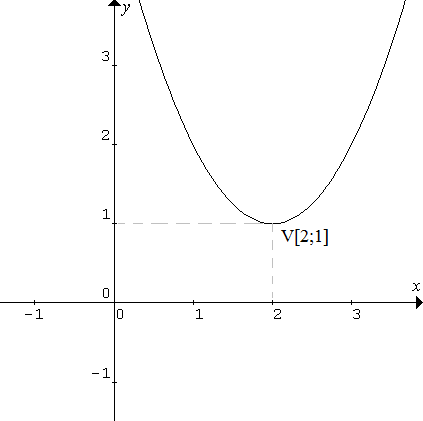
Bod V[2; 3] na obrázku je v tomto prípade minimom funkcie a nazývame ho vrchol paraboly.
Pri určovaní súradníc vrchola V môžeme postupovať dvoma spôsobmi:
- úpravou na štvorec, kde využijeme v pozmenenom tvare vzťah (a ± b)2 = a2 ± 2ab + b2
- (a ± b)2 – b2 = a2 ± 2ab (o chvíľu si to ukážeme na konkrétnom príklade)
- alebo rýchlejšiu formu – zapamätať si že x-ová súradnica vrchola je -b/2a a y-ovú súradnicu dopočítame dosadením do predpisu funkcie
- V[-b/(2a); f(-b/(2a))]
A ako určíme priesečník s y-ovou osou?
Ak máme predpis kvadratickej funkcie upravený na tvar: y = ax2 + bx + c, tak priesečník s osou y Py = [0; c].
Ak si to nezapamätáte, tak používajte už naučené: Py=[0;y] a y-ovú súradnicu priesečníka určíme dosadením čísla 0 za x do predpisu kvadratickej funkcie.
Skúste prejsť na Kreslič kvadratickej funkcie a nakresliť grafy funkcií f: y = x2 – 4x + 5 a g: y = -x2 – 4x + 5.
Zmenil sa graf funkcie? Ako? Skúste porovnať predpisy oboch funkcií, čím sa líšia?
Čo potrebujeme vedieť pri náčrte kvadratickej funkcie?
Ak potrebujeme iba jednoduchý náčrt kvadratickej funkcie, tak potrebujeme poznať:
- tvar paraboly
- vrchol paraboly
- priesečník Py so súradnicovou osou y
Zdá sa vám, že sme ešte nespomínali tvar paroboly?
Predpokladám, že ste boli všetci šikovní a pri vykreslení oboch parabol v Kresliči kvadratickej funkcie ste zistili, že pre a>0 je tvar ∪ a pre a<0 máme tvar ∩.
A teraz ukážkový príklad.
Príklad 1:
Načrtnite graf funkcie f: y = x2 – 2x + 3.
Riešenie:
Povedali sme si, že potrebujeme vedieť tvar, súradnice vrchola a priesečník s osou y.
Vypíšme si všetky koeficienty:
a = 1; b = -2; c = 3
Keďže koeficient a = 1, tak tvar už máme … ∪
V = [-b/(2a); f(-b/(2a))] … -b/(2a) = -(-2)/(2·1) = 1
-b/(2a) = -(-2)/(2·1) = 1 f(-b/(2a)) = 12 – 2·1 + 3 = 2
Teda V = [1; 2]
Py = [0; c] = [0; 3]
… a načrtneme graf
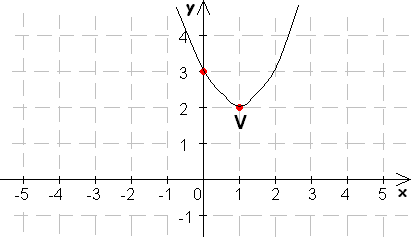
A ako by sme určili súradnice vrchola „úpravou na štvorec“?
a2 – 2ab + b2 = (a – b)2 /-b2
a2 – 2ab = (a – b)2 – b2
Z predpisu y = x2 – 2x + 3 teda podľa vyššie uvedeného pozmeného vzťahu upravíme časť x2 – 2x.
y = x2 – 2x + 3 = (x – 1)2 – 1 + 3 = (x – 1)2 + 2
x-ová súradnica vrchola je taká hodnota premennej x, kde x – 1 = 0 teda xV = 1
y-ová súradnica vrchola je číslo za zátvorkou teda yV = 2
Takže V = [1; 2].
O vlastnostiach kvadratickej funkcie (monotónnosť, ohraničenosť, parita, extrémy, …) si povieme nabudúce.
