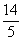Lineárna funkcia je funkcia daná rovnicou y = ax + b , kde a, b sú reálne čísla.
Grafom lineárnej funkcie je priamka alebo jej časť. Na zostrojenie grafu lineárnej funkcie nám stačí poznať súradnice dvoch jej bodov.
Príklad 1:
Zostrojte graf funkcie y=2x-1.
Riešenie:
Vhodne si zvolíme x-ové súradnice dvoch bodov funkcie a dosadením do predpisu funkcie dopočítame y-ové súradnice týchto bodov.
| x | -1 | 1 |
| y | -3 | 1 |
Tým sme získali súradnice dvoch bodov patriacich grafu danej priamky. Obrazy týchto bodov znázorníme v karteziánskej súradnicovej sústave a následne zakreslíme graf lineárnej funkcie.
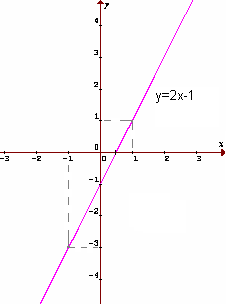
Definičným oborom tejto lineárnej funkcie sú všetky reálne čísla. ( D(f) = R )
Oborom hodnôt tejto lineárnej funkcie sú všetky reálne čísla. ( H(f) = R )
Priesečníky grafu so súradnicovými osami:
Uvažujme lineárnu funkciu f z predošlého zadania, danú predpisom y = 2x – 1.
a) Priesečník s osou x:
- všetky body ležiace na osi x majú y-ovú súradnicu nulovú, preto priesečník s osou x bude bod Px = [x; 0].
- dosadíme teda do predpisu lineárnej funkcie y-ovú súradnicu bodu Px:
- riešením jednoduchej rovnice sme získali x-ovú súradnicu priesečníka
- hľadaný priesečník s osou x-ovou je teda bod P[0,5;0].
- všimnime si: priesečník s osou x-ovou je bod Px[-b/a;0]
| Konkrétne | Všeobecne | |||||||
| 0 | = | 2x – 1 | /+1 | 0 | = | ax + b | /-b | |
| 1 | = | 2x | /:2 | -b | = | ax | /:a | |
| 0,5 | = | x | -b/a | = | x | |||
b) Priesečník s osou y
- všetky body ležiace na osi y majú x-ovú súradnicu nulovú, preto priesečník s osou y bude bod Py = [0; y].
- dosadíme teda do predpisu lineárnej funkcie x-ovú súradnicu bodu Py:
- riešením jednoduchej rovnice sme získali y-ovú súradnicu priesečníka
- hľadaný priesečník s osou y-ovou je teda bod P[0;-1].
- všimnime si: priesečník s osou y-ovou je bod Py[0;b]
| Konkrétne | Všeobecne | |||||||
| y | = | 2·0 – 1 | y | = | a·0 + b | |||
| y | = | -1 | y | = | b | |||
Špeciálne prípady lineárnej funkcie:
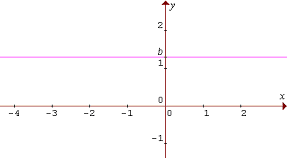
1. Konštantná funkcia:
Ak v predpise lineárnej funkcie y = ax + b je a = 0, potom y = b. V tomto prípade hovoríme o tzv. konštatnej funkcii, ktorej grafom je priamka rovnobežná s osou x a prechádzajúca bodom [0; b].
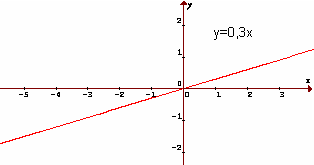
2. Priama úmernosť:
Ak v predpise lineárnej funkcie y = ax + b je b = 0, potom y = ax. V tomto prípade hovoríme o tzv. priamej úmernosti, ktorej grafom je priamka, ktorá vždy prechádza začiatkom súradnicového systému, teda bodom [0; 0].
Vlastnosti lineárnej funkcie:
- lineárna funkcia je rastúca práve vtedy, keď a > 0;
- lineárna funkcia je klesajúca práve vtedy, keď a < 0;
Príklad 2:
Je daná lineárna funkcia f: y=ax+b. Určte lineárnu funkciu g, ktorej graf je súmerný s grafom funkcie y=ax+b podľa:
- osi x
- osi y
- začiatku súradnicovej sústavy
Riešenie:
a) Ak má byť graf súmerný podľa osi x, tak
- bude podobne ako graf funkcie y=ax+b prechádzať bodom Px[-b/a;0]
- ak graf funkcie f pretína y-ovú os v bode [0;b], potom graf funkcie g bude pretínať y-ovú os v bode [0;-b].
Teda funkcia g bude mať nasledovný predpis: y=-ax-b.
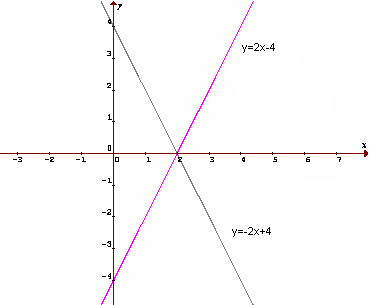
b) Ak má byť graf súmerný podľa osi y, tak
- bude podobne ako graf funkcie y=ax+b prechádzať bodom Py[0;b]
- ak graf funkcie f pretína x-ovú os v bode [-b/a;0], potom graf funkcie g bude pretínať x-ovú os v bode [b/a;0].
Teda funkcia g bude mať nasledovný predpis: y=-ax+b.
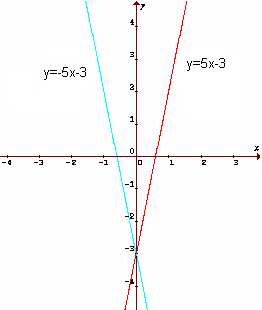
c) Ak má byť graf súmerný podľa začiatku súradnicovej sústavy, tak
- ak graf funkcie f pretína y-ovú os v bode [0;b], potom graf funkcie g bude pretínať y-ovú os v bode [0;-b]
- ak graf funkcie f pretína x-ovú os v bode [-b/a;0], potom graf funkcie g bude pretínať x-ovú os v bode [b/a;0]
Teda funkcia g bude mať nasledovný predpis: y=ax-b.
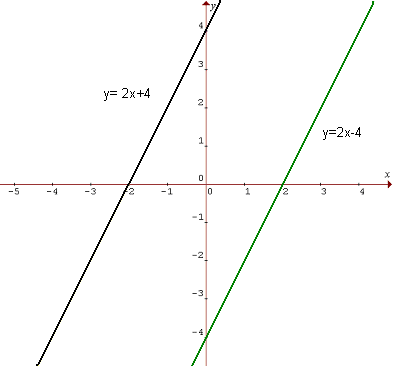
Všimnime si:
Všeobecne platí: Ak sú dané dve funkcie f: y=rx+s a g: y=kx+q, potom sú:
- súmerné podľa osi x-ovej, ak r=-k a zároveň s=-q, napr. f: y=2x-4 a g: y=-2x+4; (obr. v príklade 2a)
- súmerné podľa osi y-ovej, ak r=-k a zároveň s=q, napr. f: y=5x-3 a g: y=-5x-3; (obr. v príklade 2b)
- súmerné podľa začiatku súradnicovej sústavy (ich grafy sú rovnobežné), ak r=k a zároveň s=-q, napr. f: y=2x-4 a g: y=2x+4; (obr. v príklade 2c)
- ich grafy sú rovnobežné rôzne, ak r=k a zároveň s≠q, napr. f: y=2x-4 a g: y=2x+1; (nasledovný obr.)
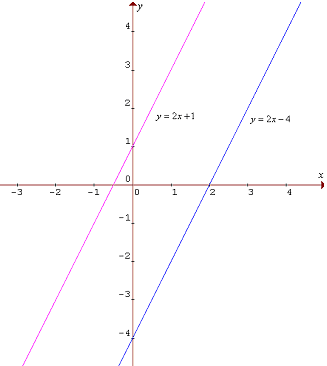
Zostrojte graf danej funkcie, určte je definičný obor, obor hodnôt a priesečníky grafu funkcie so súradnicovými osami, ak:
- f: y = 2x + 1, ak x ∈ (-2; ∞)
- g: y = -x + 2, ak x ∈ (-3; 4>
- h: y = -3x – 4, ak x ∈ (-2; 2)
Riešenie:
a) zo zadania vyplýva, že D(f) = (-2; ∞); najskôr si určíme funkčné hodnoty v x = -2 a ďalšom x ∈ (-2; ∞), napr. x=1
f(-2)=2·(-2)+1=-3; f(1)=2·(1)+1=3, čo môžeme prehladne zapísať do tabuľky:
| x | -2 | 1 |
| y | -3 | -3 |
Zostrojíme graf: (nezabudnite na prázdny krúžok pri znázornení bodu [-2;2] lebo tento bod grafu nepatrí)
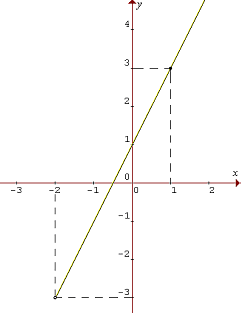
- D(f) = (-2; ∞); H(f) = (-3; ∞)
- Px[-0,5;0]; Py[0;1]
b) zo zadania vyplýva, že D(f) = (-3; 4>; najskôr si určíme funkčné hodnoty v x=-3 a x=4 (čiže v krajných bodoch intervalu)
f(-3)=-(-3)+2=5; f(4)=-4+2=-2 teda v tabuľke
| x | -3 | 4 |
| y | 5 | -2 |
Zostrojíme graf: (nezabudnite na prázdny krúžok pri znázornení bodu [-3;5] lebo tento bod grafu nepatrí, ale bod [4;-2] grafu patrí, teda krúžok bude plný)
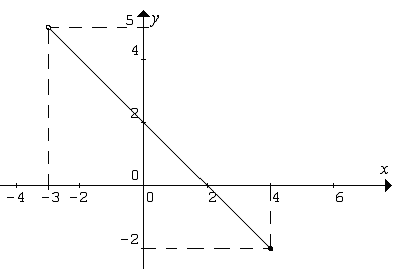
- D(f) = (-3;4 >; H(f) = <-2;5)
- Px[2;0]; Py[0;2]
c) zo zadania vyplýva, že D(f) = (-2; 2); najskôr si určíme funkčné hodnoty v x=-2 a x=2 (čiže v krajných bodoch intervalu)
f(-2)=-3·(-2)-4=2; f(1)=-3·2-4=-10
| x | -2 | 2 |
| y | 2 | -10 |
Zostrojíme graf: (nezabudnite na prázdny krúžok pri znázornení bodov [-2;2] a [2;-10] lebo tieto body grafu nepatria)
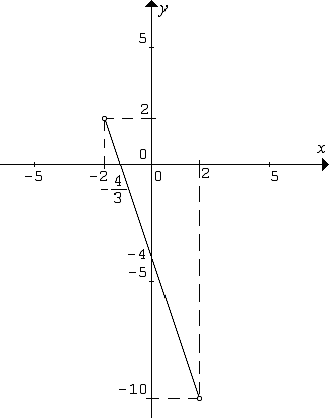
- D(f) = (-2;2); H(f) = (-10;2)
- Px[-
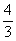 ;0]; Py[0;-4]
;0]; Py[0;-4]
Príklad 4:
Určte lineárnu funkciu, pre ktorú platí: f(-2) = 6; f(3) = -2.
Riešenie:
Všeobecný predpis lineárnej funkcie je y = ax + b.
- Zo zadania vyplýva:
- ak x = -2, potom y = 6
- ak x = 3, potom y = -2
Dosadením do predpisu funkcie dostaneme sústavu dvoch rovníc s dvoma neznámymi: ( ako riešiť sústavu dvoch rovníc s dvoma neznámymi)
| 6 | = | a·(-2) + b | /·(-1) |
| -2 | = | a·3 + b | |
| -6 | = | 2a – b | |
| -2 | = | 3a + b | (využijeme sčítaciu metódu) |
| -8 | = | 5a | /:5 |
– 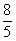 |
= | a | |
Ďalej pokračujeme vyjadrením b napr. z prvej rovnice:
b = 2a + 6 = 2·(- 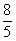 ) + 6 = –
) + 6 = – 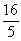 + 6 =
+ 6 = 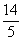
Po dosadení do všeobecného predpisu funkcie teda dostaneme:
y = – 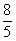 x +
x + 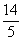
Výsledok: Predpis funkcie je y = – 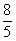 x +
x +