Obsah článku:
↑ Hore
Na názornú predstavu množín, množinových vzťahov a operácií medzi množinami sa používajú ich grafické znázornenia v rovine, tzv. množinové diagramy.
Základná množina Z sa znázorňuje spravidla obdĺžnikom a jej podmnožiny A, B, … ako kruhy alebo iné zvyčajne oválne obrazce vnútri obdĺžnika. Tieto grafické znázornenia sa nazývajú Vennove diagramy.
K znázorneniu množín reálnych čísel sa zvyčajne používa číselná os.
Príklad 1:
- Daná je základná množina Z = {1,2,3,…,9} a jej podmnožiny A = {1,2,3,4,5} a B = {3,6,9}. Znázornite pomocou Vennovych diagramov a zapíšte vymenovaním prvkov nasledovné množiny:
- a) doplnok množiny A vzhľadom k množine Z
- b) A∪B
- c) A∩B
- d) A-B
- Riešenie:
- a) Doplnok množiny A vzhľadom k množine Z tvoria všetky prvky patriace množine Z a zároveň nepatriace množine A, čiže:
- A‘Z={6,7,8,9}
-
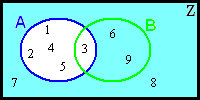
- b) A∪B={1.2.3.4.5.6.9}
-
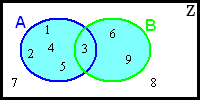
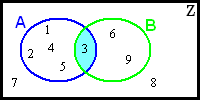
- c) A∩B={3}
-
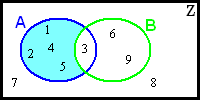
- d) A-B={1.2.4.5}
-
Príklad 2:
- Dané sú množiny A, B, C. Pomocou Vennovych diagramov zistite, či platia nasledovné rovnosti:
- a) (A∪B)’=A’∩B‘
- b) A-B=B‘-A‘
- c) (A∪B)’∪(A∩B)=(A-B)’∩(B-A)‘
- d) C’∩(AΔB)=[B-(A∪C)]∪[A-(B∪C)]
Riešenie:
Pri používaní Vennovych diagramov je dobré používať šrafovanie rôznymi farbami, pozorne sledujte riešenie tohto príkladu.
Klikaním na tlačidlo “Rieš„ sa bude vykresľovať riešenie príslušného príkladu:
