Výroková formula

K tejto téme je dostupný aj Test a Vysvetlenie učiva

Neriešené príklady

Príklad 1:

Určte pravdivostné hodnoty zložených výrokov:

1. (A ∧ B)’ ∨ (A ⇒ B)
2. (A ⇒ B) ∧ (A ⇔ B)’
3. (A’ ∨ B’) ⇔ (A ∧ B)
4. ((A ∨ B) ⇔ (A’ ∨ B’))’
5. (A ∧ B) ∨ (A ⇒ B)
6. (A ⇔ B) ∧ (A ⇒ B)
7. (A’ ⇒ B) ∨ (A’ ∧ B)
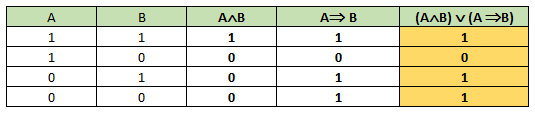
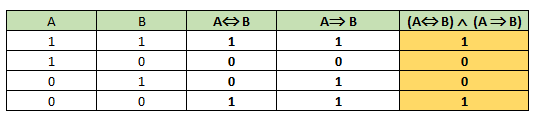
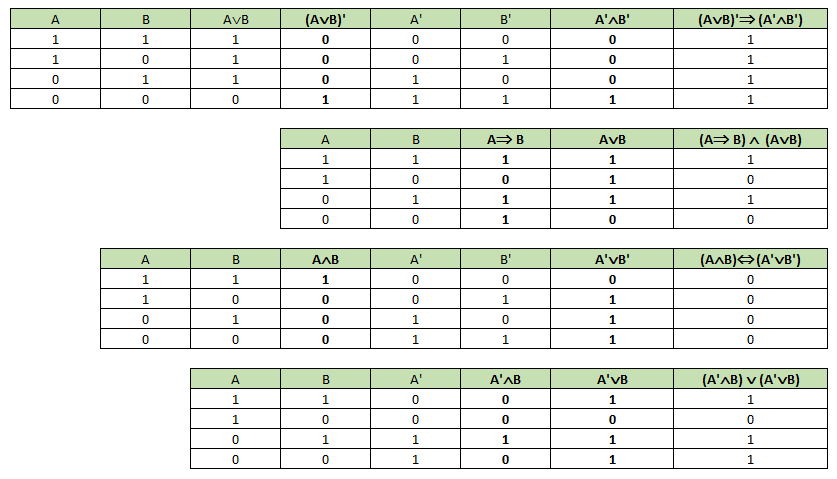
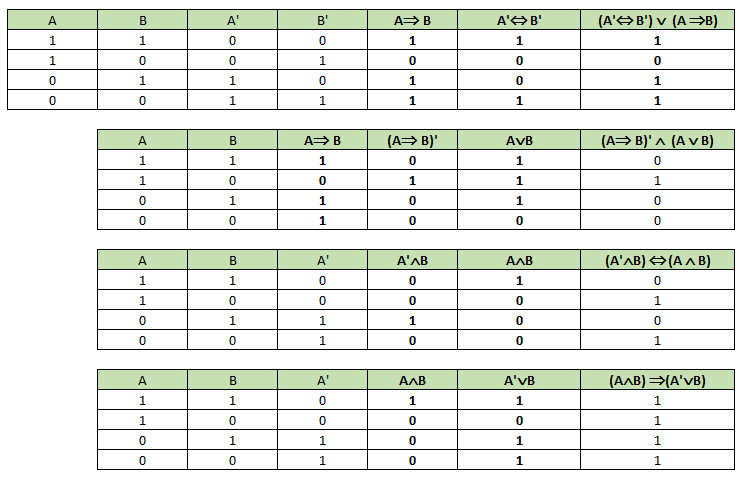
8. (A ∧ B’) ⇒ (A ⇔ B)

---

Príklad 2:

Nájdi a oprav chyby v Tabuľke pravdivostných hodnôt. Je aj po opravení chýb daná výroková formula tautológiou?

p	q	p∨p	p∧p	¬(p∨p)	(p⇔p)∨p	(p⇔p)∨p) ⇔ ¬(p∨p)
1	1	1	1	1	1	1
1	1	1	1	1	1	1
1	1	1	1	1	1	1
1	1	1	1	1	1	1

---

 Príklad 3:

Zistite, či dané výrokové formuly predstavujú tautológie:

1. (¬A ⇔ ¬B) ∨ (A ⇒ B)
2. ¬(A ⇒ B) ∧ (A ∨ B)
3. (¬A ∧ B) ⇔ (A ∧ B)
4. (A ∧ B) ⇒ (A’ ∨ B)
5. (¬A ∧ B) ⇒ (A ⇒ B)
6. (A ⇔ ¬B) ∨ (A ⇒ B)
7. (A’ ⇒ B) ∨ (A’ ∧ B)
8. (A ∧ B’) ⇒ (A ⇔ B)

---

 Príklad 4:

Ktoré z daných výrokových formúl sú kontradikcie?

1. ¬(A ∨ B) ⇒ (¬A ∧ ¬B)
2. (A ⇒ B) ∧ (A ∨ B)
3. (A ∧ B) ⇔ (¬A ∨ ¬B)
4. (¬A ∧ B) ∨ (A’ ∨ B)
5. (A ∧ B) ⇔ (A ⇒ B)
6. (A ⇒ B) ∧ (A ⇒ B)
7. (A ⇒ B) ⇔ (A ∨ B)
8. (A ∧ B) ⇒ (A ⇔ B)

---