Príklad č. 1
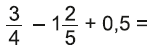
Vypočítajte a výsledok napíšte v tvare desatinného čísla.
Riešenie:

Výsledok: -0,15
Príklad č. 2
Máme číslo A = 753 672.
Vypočítajte rozdiel čísla A zaokrúhleného na stovky a čísla A zaokrúhleného na desaťtisíce.
Riešenie:
číslo A zaokrúhlené na stovky: 753 700
číslo A zaokrúhlené na desaťtisíce: 750 000
Rozdiel: 753 700 – 750 00 = 3 700
Výsledok: 3 700
Príklad č. 3
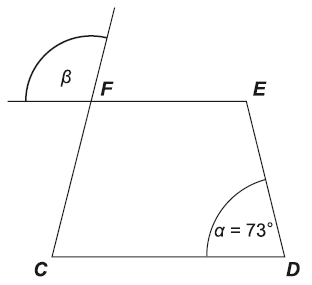
Na okbrázku je znázornený rovnoramenný lichobežník CDEF. Veľkosť uhla α je 73°. Vypočítajte v stupňoch veľkosť uhla β.
Riešenie:
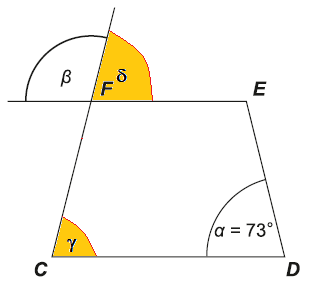
Do obrázka si doplníme uhly γ a δ.
Keďže lichobežník je rovnoramenný, tak γ = α = 73°.
Uhly γ a δ sú súhlasné, preto δ = 73°.
Uhly β a δ sú susedné, preto β = 180° – 73° = 107°
Výsledok: 107°
Príklad č. 4
Štvorec JKLM má strany dĺžky 24 cm. Bod S je stredom strany LM. Vypočítajte obsah štvoruholníka JKSM v cm2.
Riešenie:
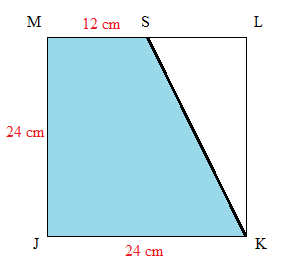
Keďže bod S je stredom strany LM, tak dĺžka SM je 12 cm. Štvoruholník JKSM je zároveň pravouhlým lichobežníkom, ako vidíte na obrázku.
Jeho obsah vypočítame pomocou vzorca pre výpočet obsahu lichobežníka:
S = (a+c)⋅v / 2, kde a = JK, c = SM, v = JM
S = (24+12)⋅24 / 2 = 432 cm2
Výsledok: 432
Príklad č. 5
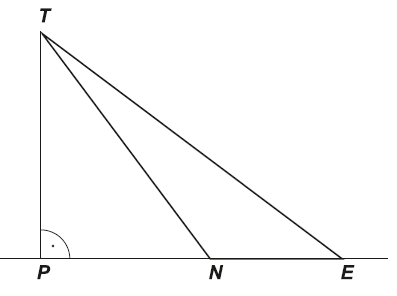
Na obrázku je znázornený trojuholník NET. Bod P je päta výšky tohto trojuholníka z vrcholu T na stranu NE; bod N leží na úsečke PE.
Vieme, že:
|PE| = 16 cm
|TP| = 12 cm
|TE| = 20 cm
|NE| = 7 cm
Zistite obvod trojuholníka NET v cm.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 42
Príklad č. 6
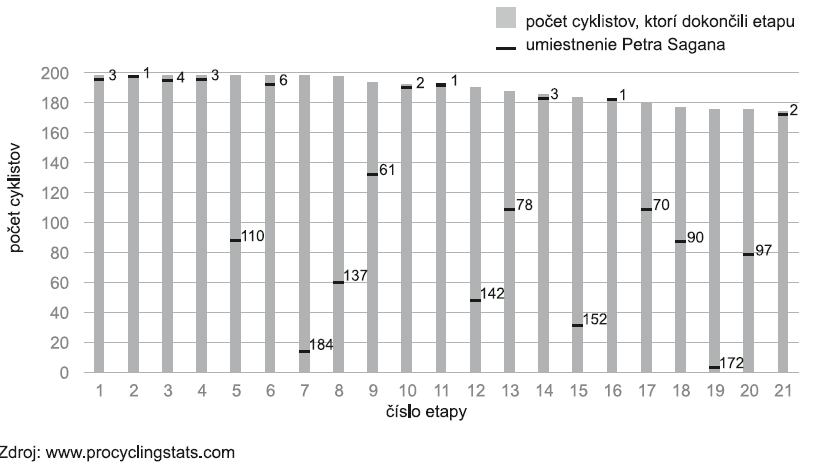
V stĺpcovom diagrame je znázornené umiestnenie Petra Sagana v jednotlivých etapách Tour de France v roku 2016. Všetkých etáp bolo spolu 21. Koľko percent zo všetkých etáp predstavujú tie etapy, v ktorých skončil na 1. až 3. mieste?
Výsledok zaokrúhlite na celé číslo.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 38
Príklad č. 7
Reštaurácia bola v čase obeda plne obsadená. Kým v reštaurácii obsluhovali len traja čašníci, hostia čakali na obedové menu v priemere 45 minút. Koľko minút v priemere budú hostia čakať, ak sa k trom obsluhujúcim čašníkom pridajú ešte ďalší dvaja čašníci obsluhujúci rovnako rýchlo?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 27
Príklad č. 8
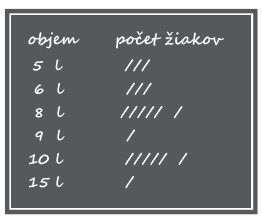
Na hodine fyziky žiaci odhadovali objem smetného koša v triede. Na tabuli je záznam odpovedí 20 žiakov. Skutočný objem tohto smetného koša bol 12 litrov. O koľko litrov sa od tejto hodnoty líši priemerný žiacky odhad?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 3,75
Zadanie AQUAPARK
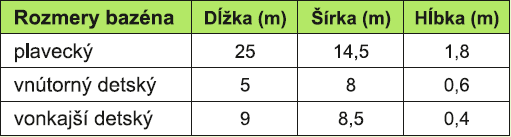
V aquaparku sú rôzne bazény: jeden vírivý, jeden plavecký a dva detské. Odporúčaná doba pobytu vo vírivom bazéne je 15 minút a môžu v ňom byť maximálne 4 osoby. Plavecký a detské bazény majú tvar kvádra a ich rozmery sú uvedené v tabuľke.
Na zadanie AQUAPARK sa vzťahujú úlohy 09 a 10.
Príklad č. 9
Najviac koľko osôb sa môže vystriedať vo vírivom bazéne za 2 hodiny, ak bude dodržaný aj maximálny počet osôb, aj odporúčaná doba pobytu v tomto bazéne?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 32
Príklad č. 10
Pri napúšťaní vnútorného detského bazéna bol kvôli poruche vypnutý prívod vody práve vo chvíli, keď bolo v tomto bazéne napustených 15,6 m3 vody. Koľko percent z celkového objemu tohto bazéna bolo napustených do momentu vypnutia prívodu vody?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 65
Príklad č. 11
Brigádnici Ivan, Lea a Dana zarobili spolu 480 eur. Ivan zarobil tretinu z týchto peňazí. Zvyšné peniaze zarobili Lea a Dana v pomere 3:1. Koľko eur zarobila Lea?
A: 240 €
B: 120 €
C: 320 €
D: 80 €
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 12
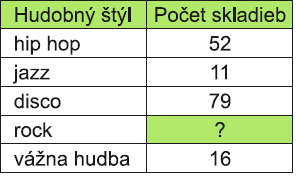
Zuzana má v mobilnom telefóne 5 priečinkov s rôznymi hudobnými štýlmi. V tabuľke sú uvedené ich názvy a počty skladieb, ktoré obsahujú. Doplňte chýbajúce číslo tak, aby pri funkcii náhoidného prehrávania hrala rocková skladba s pravdepodobnosťou 21% ako prvá.
A: 21
B: 32
C: 36
D: 42
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
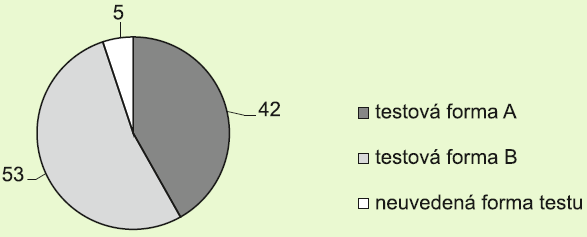
Vstupný test z chémie vo forme A alebo B riešilo spolu 100 žiakov. Každý z nich mal v odpoveďovom hárku uviesť, ktorú formu testu riešil. Piati žiaci to neurobili.
V kruhovom diagrame na obrázku je znázornené rozdelenie testovaných žiakov podľa toho, ktorú formu testu uviedli.
Pri analýze testovanej vzorky žiakov boli vyslovené dve tvrdenia:
- Je možné, že formu A riešilo o 6 žiakov menej ako formu B.
- Je možné, že formu B riešilo o 11 žiakov viac ako formu A.
Príklad č. 13
Posúďte pravdivosť týchto tvrdení a vyberte správnu odpoveď.
A: Len prvé tvrdenie je pravdivé.
B: Len druhé tvrdenie je pravdivé.
C: Obidve tvrdenia sú pravdivé.
D: Obidve tvrdenia sú nepravdivé.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 14
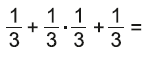
A: 0,8
B: 0,7
C: 0,5
D: 0,4
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 15
Vyberte mocninu, ktorá má najvyššiu hodnotu.
A: 52
B: 43
C: 34
D: 25
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Najčastejšie formáty papiera majú označenie pozostávajúce z písmena a číslice, napr. A4.
Základným formátom radu A je A0. Ďalšie formáty tohto radu (A1, A2, A3, …) vznikajú postupným strihaním listu papiera na polovicu, kolmo na dlhšiu stranu.
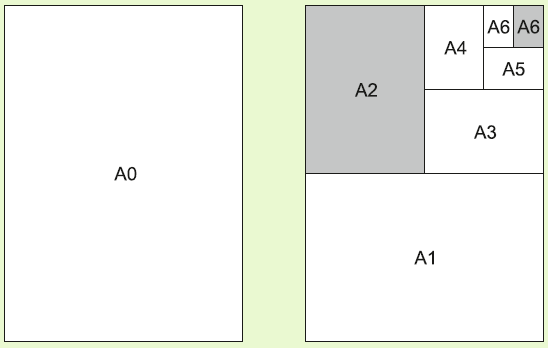
Príklad č. 16
Najviac na koľko papierov formátu A6 možno rozstrihnúť papier formátu A2?
A: 8
B: 16
C: 32
D: 64
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 17
Drevenú kocku s hranou dĺžky 4 cm sme natreli po celom povrchu zelenou farbou. Potom sme ju rozrezali na malé kocky s hranou dĺžky 1 cm. Počet kociek, ktoré majú práve dve steny zafarbené nazeleno je
A: 8
B: 12
C: 16
D: 24
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 18
Na ľavej strane rovnice je výraz x-2,4. Zistite, ktorý z výrazov patrí na pravú stranu rovnice, aby rovnica mala koreň x = 2,8.
A: 3 ⋅ (x – 1,1)
B: 2 ⋅ (3 – x)
C: 3 ⋅ (x + 1,1)
D: 2 ⋅ (3 + x)
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Zadanie KÚPA BYTU

Manželia Novákovci sa rozhodli pre kúpu bytu. V realitnej kancelárii im ponúkli 4 voľné byty. Údaje o jednotlivých bytoch sú uvedené v tabuľke.
Na zadanie KÚPA BYTU sa vzťahujú úlohy č. 19 a 20.
Príklad č. 19
Pani Nováková navrhovala byt č. 2, lebo podľa nej má zo všetkých ponúkaných bytov najnižšiu cenu za 1 m². Pán Novák navrhoval byt č. 3, lebo je najlacnejší.
Ktorý z nich správne odôvodnil svoj návrh?
A: Len pani Nováková.
B: Len pán Novák.
C: Obidvaja.
D: Ani jeden.
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Riešenie:
Výsledok: C
Príklad č. 20
Nakoniec sa rozhodli pre dvojizbový byt v pôvodnom stave. Vybrali si ten s väčšou rozlohou. Majú našetrených 17 000 eur, zvyšnú časť ceny si požičajú od banky. Splácať budú 120 eur mesačne po dobu 15 rokov. O koľko eur zaplatia banke viac oproti požičanej sume?
A: 4 600 €
B: 5 400 €
C: 6 200 €
D: 6 600 €
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Riešenie:
Výsledok: D
Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.