Príklad č. 1
Nájdite číslo, ktoré po vydelení číslom 12 dáva podiel 57 a zvyšok 11.
Riešenie:
Postupne zapisujeme podľa zadania:
Nájdite číslo …… x
ktoré po vydelení číslom 12 …… x : 12
dáva podiel 57 a zvyšok 11 …… x : 12 = 57 zv. 11
Pamätáte si, ako ste robili skúšku správnosti?
x = 57 ⋅ 12 + 11
A vyriešime:
x = 57 ⋅ 12 + 11 = 684 + 11 = 695
Výsledok: 695
Príklad č. 2
V sude je 1,5 hektolitra dažďovej vody. Pri polievaní záhrady sa zo suda minuli dve pätiny vody. Koľko litrov vody zostalo v sude?
Riešenie:
zo suda sa minuli 2/5 z 1,5 hl … 2/5 ⋅ 1,5 hl = 0,6 hl
v sude bolo 1,5 hl
zostalo … 1,5 hl – 0,6 hl = 0,9 hl = 90 l
Výsledok: 90
Príklad č. 3
V mliekarni využívajú pri dávkovaní jogurtov novú a starú linku. Dávkovaním jogurtov na starej linke je objednávka splnená za 6 hodín. Ak pracujú obe linky spoločne, splnia takú istú objednávku za 2 hodiny. Koľko hodín bude trvať splnenie takejto objednávky, ak sa budú jogurty dávkovať len na novej linke?
Riešenie:
stará linka ….. 6 hodín
obe linky spoločne …… 2 hodiny
nová linka …… x hodín
Prevedieme na množstvo práce, ktorú linky zvládnu za 1 hodinu:
stará linka … 1/6
nová linka …. 1/x
spoločne …… 1/2
A zostavíme rovnicu:
1/6 + 1/x = 1/2 /⋅6x
x + 6 = 3x /-3x-6
-2x = -6 /:(-2)
x = 3
Výsledok: 3
Príklad č. 4
Na jar žiaci čistia miestny potok od odpadkov. Traja žiaci vyčistia za 1 hodinu priemerne 10 metrov dĺžky potoka. Koľko metrov dĺžky potoka priemerne vyčistí 18 rovnako šikovných žiakov za 4 hodiny?
Riešenie:
Najskôr vypočítame, koľko metrov dĺžky potoka vyčistia 18 žiaci za 1 hodinu.
3 žiaci za 1 hodinu …….. 10 m
18 žiakov za 1 hodinu …… x m
Ide o priamu úmernosť, preto:
18:3 = x:10
18⋅10 = 3⋅x
180 = 3x /:3
x = 60
Za 4 hodiny ….. 60⋅4 = 240 m
Výsledok: 240
Príklad č. 5
Odvesny pravouhlého trojuholníka majú dĺžku 1,2 dm a 1,6 dm. Vypočítajte obvod tohto pravouhlého trojuholníka v decimetroch.
Riešenie:
Aby sme mohli vypočítať obvod tohto trojuholníka, potrebujeme poznať dĺžku prepony (označme x). Pri jej výpočte využijeme Pytagorovu vetu:
x2 = 1,22 + 1,62
x2 = 1,44 + 2,56
x2 = 4
po odmocnení
x = 2
Obvod trojuholníka = súčet jeho strán
o = 1,2 + 1,6 + 2 = 4,8 dm
Výsledok: 4,8
Príklad č. 6
Na obrázku je vrchná doska konferenčného stola v tvare šesťuholníka. Na túto vrchnú dosku chce Karol nalepiť farebnú fóliu. Aký obsah bude mať nalepená fólia? Výsledok vyjadrite v m2.
Pre šesťuholník platí:
|AE| = 0,6 m, |FC| = 1,2 m, |AB| = |ED| = 0,8 m, AB || FC || ED.
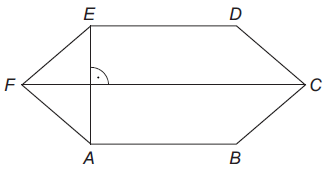
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 0,6
Príklad č. 7
Štvorboký hranol má rozmery uvedené na obrázku. Z neho bol odrezaný trojboký hranol znázornený sivou farbou. Koľko m3 má zvyšná časť hranola?
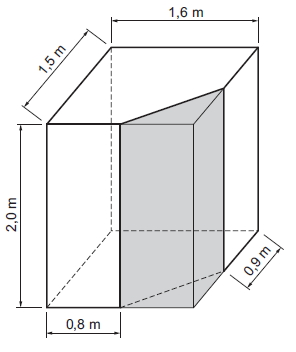
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 4,32
Príklad č. 8
Podlaha obývacej izby v tvare obdĺžnika má obsah 30,6 m2 a šírku 5,1 m. Koľko centimetrov meria obvod podlahy obývacej izby na pláne s mierkou 1 : 150?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 14,8
Príklad č. 9
Motocyklista ide rýchlosťou 48 km/h. Koľko kilometrov prejde touto rýchlosťou za 40 minút?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 32
Príklad č. 10
Z vkladu 2 000 € bol úrok za jeden rok 18 €. Aká bola ročná úroková miera v percentách?
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: 0,9
Príklad č. 11
Riešením rovnice (5a-11)/3 = a – 4 je číslo:
A: -0,5 B: 0,5 C: 3,5 D: -7,5
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 12
Na každej číselnej osi sú zobrazené tri čísla. V ktorej z možností sú na číselnej osi správne zobrazené všetky tri čísla?

Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 13
V triede je dvadsaťštyri žiakov. V piatok sa na hodine matematiky delia na dve skupiny po dvanásť žiakov.Vtabuľke sú výsledky hodnotenia žiakov v druhej skupine.
| Hodnotenie (známka) | Počet žiakov |
| Výborný (1) | 2 |
| Chválitebný (2) | 3 |
| Dobrý (3) | 6 |
| Dostatočný (4) | 1 |
| Nedostatočný (5) | 0 |
Traja žiaci v prvej skupine majú o stupeň horšiu známku ako žiaci v druhej skupine, ostatní žiaci mali rovnaké hodnotenie.Aký je aritmetický priemer známok všetkých žiakov prvej skupiny?
A: 3,5 B:2,75 C:2,5 D: 2,25
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 14
Martina pomáhala trénerovi vypisovať diplomy. Vypísanie prvého diplomu jej trvalo 3 minúty, vypísanie každého ďalšieho 2 minúty. Koľko minút jej bude trvať vypísanie diplomov (včítane prvého), ak bude pracovať takýmto tempom?
A: 5n + 3
B: 3n + 2
C: 2n + 3
D: 2n + 1
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: D
Príklad č. 15
Pre ktoré najmenšie prirodzené číslo k platí, že zlomok 3/5 je menší ako zlomok k/40?
A: 26
B: 25
C: 24
D: 23
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 16
Zostrojte rovnobežník ABCD. Dané sú rozmery |AB| = 5 cm, |BC| = 5,5 cm, uhol BAC má veľkosť 45°. Odmerajte dĺžku uhlopriečky BD v milimetroch. Ktoré z nasledujúcich tvrdení o dĺžke uhlopriečky BD je pravdivé?
A: 53 ? |BD| ? 57
B: 70 ? |BD| ? 74
C: 75 ? |BD| ? 79
D: 95 ? |BD| ? 99
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: B
Príklad č. 17
Trieda si vytvorila vlastný erb, ktorý mal tvar zložený z rovnoramenného lichobežníka ABCD a polkruhu so stredom S a priemerom AB. Lichobežník tvorili tri zhodné rovnoramenné trojuholníky. Polovicu polkruhu a stredné pole lichobežníka (prostredný trojuholník) žiaci vyfarbili sivou farbou. Koľko cm2 plochy erbu bolo sivej farby? Výsledok zaokrúhlite na jedno desatinné miesto.
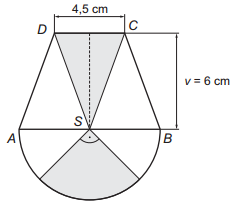
A: 77,1
B: 45,3
C: 29,4
D: 27,6
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Príklad č. 18
V tabuľke sú informácie o počte žiakov podľa počtu súrodencov.
| Počet súrodencov | 0 | 1 | 2 | 3 a viac |
| Počet žiakov | 50 | 50 | 72 | 28 |
Aká je pravdepodobnosť, že náhodne vybraný žiak má práve dvoch súrodencov?
A: 86 %
B: 50 %
C: 36 %
D: 25 %
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Príklad č. 19
V ktorej z možností je výraz x⋅(y-2) – 4⋅(2-y) správne rozložený na súčin dvoch výrazov?
A: (x + 4)·(y – 2)
B: (y – 2)·(x – 4)
C: (x – 4)·(2 – y)
D: (y + 2)·(x – 4)
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: A
Príklad č. 20
Z drevenej kocky s hranou 1 decimeter boli z dvoch rohov odrezané zhodné kocky s dĺžkou hrany 2 cm. Najviac koľko kociek s dĺžkou hrany 2 cm sa dá z drevenej kocky ešte odrezať?
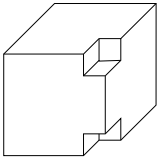
A: 117
B: 121
C: 123
D: 125
Riešenie: (dostupné pre podporovateľov pohodovamatematika.sk – zistiť viac)
Výsledok: C
Zdroj zadaní príkladov: NIVAM – Národný inštitút vzdelávania a mládeže. Texty príkladov a grafické objekty boli prepisované a NIVAM nezodpovedá za chyby vzniknuté z tohto dôvodu. Autor riešenia príkladov je Ing. Rudolf Zrebný. Za správnosť riešenia, postupu nenesie zodpovednosť NIVAM, ale autor riešenia.
