Rovnicu tvaru ax + by = c, kde a ≠ 0 alebo b ≠ 0 nazývame lineárnou rovnicou s dvoma neznámymi x, y.
Dvojicu čísel x0 a y0 nazývame riešením vyššie uvedenej rovnice, ak platí:
ax0 + by0 = c
Rovnice tvaru
ax + by = c, kde a ≠ 0 alebo b ≠ 0
dx + ey = f, kde d ≠ 0 alebo e ≠ 0
nazývame sústavou dvoch lineárnych rovníc s dvoma neznámymi x, y.
Dvojicu čísel x0 a y0 nazývame riešením vyššie uvedenej sústavy rovníc, ak platí:
ax0 + by0 = c a zároveň dx0 + ey0 = f
Pri riešení sústavy dvoch rovníc s dvoma neznámymi využívame 3 metódy:
- dosadzovaciu (substitučnú) metódu;
- sčítaciu (adičnú) metódu;
- porovnávaciu (komparačnú) metódu.
Dosadzovacia (substitučná) metóda:
Táto metóda spočíva v tom, že z jednej rovnice si vyjadríme jednu neznámu a výraz ktorý takto dostaneme, dosadíme za túto neznámu do druhej rovnice.
Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Ukážme si to radšej na jednoduchom príklade.
Príklad 1:
Riešte sústavu rovníc
| 2x – 3y = | 5 | |
| x – 2y = | 1 |
s neznámymi x, y ∈ R.
Riešenie:
Z prvej rovnice si vyjadríme napr. neznámu x:
| 2x – 3y = | 5 | / +3y |
| 2x = | 5 + 3y | /:2 |
| x = | 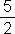 + + 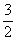 y y |
Výraz, ktorý sme získali dosadíme do druhej rovnice za neznámu x:
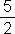 +
+ 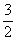 y – 2y = 1
y – 2y = 1
Získali sme lineárnu rovnicu s jednou neznámou, ktorú vyriešime:
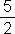 + + 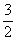 y – 2y = y – 2y = |
1 | /.2 |
| 5 + 3y – 4y = | 2 | |
| 5 – y = | 2 | /-5 |
| –y = | -3 | /·(-1) |
| y = | 3 |
Získanú neznámu dosadíme do upravenej 1. rovnice a vypočítame neznámu x:
x = 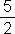 +
+ 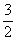 . 3 =
. 3 = 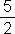 +
+ 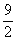 =
= 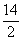 = 7
= 7
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
Ľ1 = 2 ∈ 7 – 3 ∈ 3 = 14 – 9 = 5
P1 = 5
Ľ1 = P1
Ľ2 = 7 – 2 ∈ 3 = 1
P2 = 1
Ľ2 = P2
Riešením danej sústavy je usporiadaná dvojica [x; y] = [7; 3].
Vyskúšate teraz vy? Tak poďme na to!
Príklad 2:
Sčítacia (adičná) metóda:
Táto metóda spočíva v tom, že každú rovnicu po úprave na základný tvar napr. 2x+3y=4 vhodne násobíme tak, aby po sčítaní oboch rovníc jedna neznáma „vypadla“.
Takto dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Pri „čistej“ sčítacej metóde to isté vykonáme i s druhou neznámou. V praxi je často využívaná kombinásia sčítacej a dosadzovacej metódy, čiže jednu neznámu určíme sčítacou metódou a druhú dosadením už známej hodnoty do niektorej z rovníc.
I túto metódu si radšej ukážeme na konkrétnom príklade.
Príklad 3:
Riešte sústavu rovníc
| 2x – 3y = | 5 | |
| x – 2y = | 1 |
s neznámymi x, y ∈ R.
Riešenie:
Chceme určiť napr. neznámu x, teda potrebujeme, aby „vypadla“ neznáma y. Násobíme teda prvú rovnicu číslom -2 a druhú rovnicu číslom 3.
| 2x – 3y = | 5 | / · (-2) |
| x – 2y = | 1 | / · 3 |
|
|
||
| -4x + 6y = | -10 | |
| 3x – 6y = | 3 | |
| Teraz obe rovnice sčítame: | ||
| -4x + 3x + 6y – 6y = | 3 – 10 | |
| –x = | – 7 | / · (-1) |
| x = | 7 | |
Ak chceme kombinovať sčítaciu a dosadzovaciu metódu, tak hodnotu neznámej x, ktorú sme získali, dosadíme napr. do druhej rovnice za neznámu x:
7 – 2y = 1 a z toho y = 3.
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc:
Ľ1 = 2 ∈ 7 – 3 ∈ 3 = 14 – 9 = 5
P1 = 5
Ľ1 = P1
Ľ2 = 7 – 2 ∈ 3 = 1
P2 = 1
Ľ2 = P2
Riešením danej sústavy je usporiadaná dvojica [x; y] = [7; 3].
Vyskúšate si aj sčítaciu metódu?
Príklad 4:
Porovnávacia (komparačná) metóda:
Táto metóda spočíva v tom, že z oboch rovníc si vyjadríme tú istú neznámu.
Získané výrazy porovnáme a tak dostaneme rovnicu s jednou neznámou, ktorú vyriešime. Následne dosadením vypočítame i druhú neznámu.
Vypočítajme radšej jednoduchý príklad.
Príklad 5:
Riešte sústavu rovníc
| 2x – 3y = | 5 | |
| x – 2y = | 1 |
s neznámymi x, y ∈ R.
Riešenie:
Z prvej rovnice si vyjadríme napr. neznámu x:
| 2x – 3y = | 5 | / +3y |
| 2x = | 5 + 3y | /:2 |
| x = | 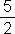 + + 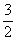 y y |
Z druhej rovnice si vyjadríme tiež neznámu x:
| x – 2y = | 1 | / +2y |
| x = | 1 + 2y |
Keďže sa rovnajú ľavé strany oboch rovníc, tak sa rovnajú i pravé strany týchto rovníc, takže vytvoríme rovnicu P1=P2, ktorú vyriešime:
| 1 + 2y = | 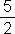 + + 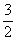 y y |
/ · 2 |
| 2 + 4y = | 5 + 3y | / – 2 – 3y |
| y = | 3 |
Získanú hodnotu premennej y dosadíme napr. do upravenej druhej rovnice:
x = 1 + 2 · 3 = 7
Skúšku správnosti robíme dosadením vypočítaných hodnôt neznámych do obidvoch rovníc podobne ako v príklade 1 a 3.
Riešením danej sústavy je usporiadaná dvojica [x; y] = [7; 3].
Príklad 6:
