Obsah článku:
Variácia k-tej triedy z n prvkov množiny M, je každá usporiadaná k-prvková skupina zostavená iba z týchto n prvkov tak, že každý sa v nej nachádza najviac raz.
Variácie k-tej triedy z n prvkov označujeme Vk(n) a vypočítame ich podľa nasledovného vzťahu:
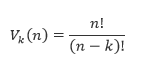
n! – čítame ako „n faktoriál“
n! = 1 . 2 . 3 … (n – 2) . (n – 1) . n pre každé celé kladné číslo n
Pri rozhodovaní, či použijeme variácie bez opakovania si odpovedáme na nasledovné otázky:
- Používame všetky prvky súčasne? Nie.
- Záleží na poradí prvkov? Áno.
- Môžu sa prvky v danej k-tici opakovať? Nie.
Pri výpočte variácií efektívne využívame krátenie faktoriálov, ktoré si ukážeme na konkrétnych príkladoch.
1. príklad:
V škole sa vyučuje 12 predmetov. Koľkými spôsobmi je možné zostaviť rozvrh hodín na pondelok, ak vieme, že žiaci majú mať 6 hodín?
Riešenie:
Je zrejmé, že budeme z celkového počtu 12 prvkov vyberať 6 prvkov. Keďže nepoužijeme všetky prvky súčasne, záleží nám na poradí vyučovacích hodín a každá vyučovacia hodina môže byť v daný deň v rozvrhu iba raz, vieme, že použijeme variácie bez opakovania.
n = 12
k = 6
V6(12) = ?
Pri výpočte rozložíme 12! tak, aby sme mohli neskôr krátiť 6!.
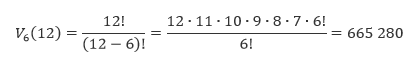
2. príklad:
Na turnaji v halovom futbale sa zúčastnilo 5 tímov. Koľko zápasov hrali v 1. kole, ak hral každý s každým? (vždy sa hral aj odvetný zápas)
Riešenie:
Z celkového počtu 5 tímov budeme vyberať 2, lebo zápas hrajú práve 2 tímy. Tzn. nepoužijeme všetky prvky súčasne. Keďže sa hrajú aj odvetné zápasy, záleží nám na poradí prvkov (tímov) v danej vybranej dvojici. Každý tím sa vo vybranej dvojici vyskytuje iba raz. Na základe uvedeného vieme, že použijeme variácie bez opakovania.
n = 6
k = 2
V2(6) = ?
Pri výpočte rozložíme 6! tak, aby sme mohli krátiť 4!.
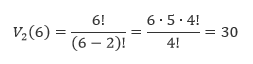
3. príklad:
Koľko je daných prvkov, ak z nich utvorených variácií druhej triedy bez opakovania je 5-krát menej ako variácií tretej triedy bez opakovania?
Riešenie:
Zo zadania si vytvoríme rovnicu:
variácií 2. triedy z n prvkov bez opak. je 5-krát menej ako variácií 3. triedy z n prvkov
V2(n) = V3(n) : 5
Danú rovnicu vyriešime.
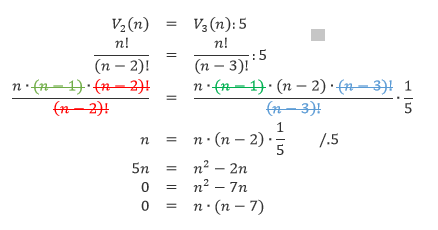
n1 = 0; n2 = 7;
Hľadaný počet prvkov je 7.
