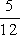Pri usporiadaní zlomkov vzostupne (od najmenšieho po najväčší) alebo zostupne (od najväčšieho po najmenší) je vhodné využiť rozširovanie a krátenie zlomkov.
Ak je to možné, upravíme všetky zlomky na základný tvar. Ďalej nájdeme najmenší spoločný násobok všetkých menovateľov porovnávaných zlomkov. Následne všetky zlomky upravíme rozšírením na spoločného menovateľa (najmenší spoločný násobok menovateľov) a usporiadame podľa veľkosti čitateľov.
Porovnávame zlomky, ktoré majú rovnaký čitateľ:
Z dvoch zlomkov, ktoré majú rovnakého čitateľa je väčší ten, ktorého menovateľ je menší.
>
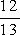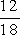lebo 13 < 18
<
lebo 9 > 3
Porovnávame zlomky, ktoré majú rôzny čitateľ i menovateľ:
V takomto prípade musíme oba zlomky najskôr pomocou rozšírenia alebo krátenia previesť na tvar s rovnakým menovateľom (alebo čitateľom) a následne porovnať podľa vyššie uvedených pravidiel.
Vhodné je oba zlomky upraviť na tvar s takým menovateľom, ktorý je najmenším spoločným násobkom pôvodných menovateľov (bližšie pozrite Najmenší spoločný násobok).
?
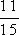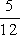
Vieme, že 15 = 5 · 3; 12 = 2 · 2 · 3 , čiže najmenším spoločným násobkom týchto čísel bude číslo 5·2·2·3 = 60. Obidva zlomky teda rozšírime na tvar s menovateľom 60.
?
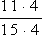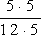
dostaneme tak zlomky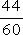 
a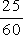 
, ktoré porovnáme.
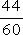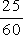>, lebo 44 > 25. Preto >.
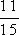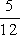Iný spôsob porovnania dvoch zlomkov je využitie krížového pravidla. Ukážeme si ho na predošlom príklade, kde sme mali porovnať zlomky ,.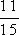
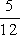Čitateľa 1. zlomku násobíme menovateľom 2. zlomku a naopak čitateľa 2. zlomku násobíme menovateľom 1. zlomku. Vzniknuté čísla porovnáme a …
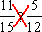…… 11 · 12 ? 5 · 15 ……. 132 > 75 preto platí
>
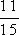