Úpravy algebraických výrazov
Úpravou algebraického výrazu rozumieme nahradenie daného výrazu iným výrazom, ktorý sa mu rovná v spoločnom definičnom obore premenných. Tento definičný obor určíme z podmienok, za ktorých má daný výraz i jeho riešenie zmysel.
Pri úpravách sa často vyžaduje úprava výrazu na súčin, zjednodušenie výrazu, odstránenie odmocniny z menovateľa, …
Pri úpravách racionálnych lomených výrazov používame vzťahy pre počítanie so zlomkami a vzťahy na rozklad mnohočlenov.
Vzorce pre druhé a tretie mocniny dvojčlenov a+b, a-b (a,b∈R resp. C):
| (a+b)2=a2+2ab+b2; (a-b)2=a2-2ab+b2; (a+b)3=a3+3a2b+3ab2+b3; (a-b)3=a3-3a2b+3ab2-b3; |
napr.: (2+3x)2=4+12x+9x2; napr.: (y-7)2=y2-14y+49; napr.: (2+5x)3=8+60x+150x2+125x3; napr.: (1-2y)3=1-6y+12y2-8y3; |
Ďalšie vzorce (a,b∈R resp. C):
| a2-b2=(a-b).(a+b); a3+b3=(a+b).(a2-ab+b2); a3-b3=(a-b).(a2+ab+b2); |
napr.: 4–9x2=(2–3x).(2+3x); napr.: 27+125x3=(3+5x).(9–15x+25x2); napr.: 8p3–27q3=(2p–3q).(4p2+6pq–9q2); |
Sčítanie a odčítanie algebraických zlomkov:
Príklad 1:
Vypočítajte: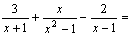 
Riešenie:
- najskôr určíme podmienky, za ktorých majú dané výrazy zmysel (v menovateli nesmie byť 0, základ druhej odmocniny musí byť ≥0);
- potom rozložíme menovatele na súčin lineárnych jedno- alebo dvojčlenov pomocou vynímania pred zátvorku alebo pomocou vyššie uvedených vzťahov;
- potom určíme spoločný menovateľ tak, že najskôr odpíšeme prvý menovateľ apostupne z každého menovateľa pridávame tie činitele, ktoré sa v spoločnom menovateli ešte nenachádzajú, čiže odpíšeme (x-1) a potom pridáme (x+1);
- následne spoločný menovateľ (x+1)(x–1) delíme menovateľom (x+1) a násobíme príslušným čitateľom 3 , teda píšeme 3∙(x–1) ; podobne spoločný menovateľ (x+1)(x–1) delíme menovateľom (x-1)(x+1) a násobíme príslušným čitateľom x , teda píšeme 1∙x čiže x ; a nakoniec spoločný menovateľ (x+1)(x–1) delíme menovateľom (x-1) a násobíme príslušným čitateľom 2 , teda píšeme 2∙(x+1) ;
- zjednodušíme čitateľ a ak sa dá, pokúsim sa upraviť ho na súčin a vykrátiť s menovateľom;
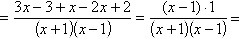
Násobenie algebraických zlomkov:
Pri násobení zlomkov násobíme čitateľa čitateľom a menovateľa menovateľom a ak chceme daný výraz zjednodušiť, tak menovateľ i čitateľ rozložíme na súčin a vykrátime.
Príklad 2:
Vypočítajte: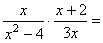 
Riešenie:
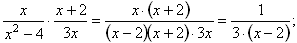; podmienky riešiteľnosti: x≠±2 ∧ x≠0
Delenie algebraických zlomkov:
pri delení dvoch zlomkov násobíme prvý zlomok prevráteným druhým zlomkom;
Príklad 3:
Vypočítajte: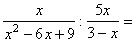 
Riešenie:
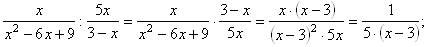; podmienky riešiteľnosti: x≠3 ∧ x≠0
Úprava zloženého algebraického zlomku:
Postupujeme buď tak, že zložený zlomok nahradíme delením dvoch zlomkov alebo podľa nasledovnej schémy (vonkajšie krát vonkajšie lomeno vnútorné krát vnútorné):
Príklad 4:
Vypočítajte: 
Riešenie:
podmienky riešiteľnosti: x≠-3 ∧ x≠0 ∧ x≠1