Priesečníky so súradnicovými osami

Priesečník s x-ovou osou má súradnice P_x = [x;0] a priesečník s y-ovou osou má súradnice P_y = [0;y].

Zistíme ich buď dosadením známej hodnoty do predpisu danej funkcie a riešením rovnice s jednou neznámou dopočítame druhú súradnicu alebo čítaním s grafu.

Príklad 1:

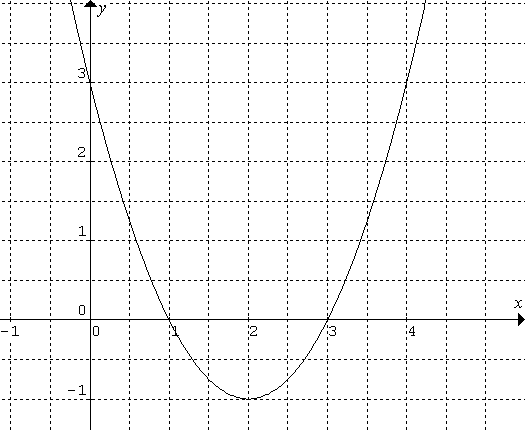
Riešenie:

a)

Vieme, že P_x=[x;0], čiže za y v predpise funkcie f dosadíme 0 a dopočítame súradnicu x.

Riešime teda rovnicu 0=2x-3. Riešením je x=1,5.

Takže priesečník s osou x-ovou je bod P_x=[1,5;0].

P_y=[0;y], čiže za x v predpise funkcie f dosadíme 0 a dopočítame súradnicu y.

Riešime teda rovnicu y=2·0-3. Riešením je y=-3.

Takže priesečník s osou y-ovou je bod P_y=[0;-3].

b)

Priamo z grafu vyplýva:

P_x1=[1;0], P_x2=[3;0], teda 2 priesečníky s osou x-ovou.

P_y=[0;3], teda jeden priesečník s osou y-ovou.

Priesečníkom so súradnicovými osami sa budete viac venovať pri jednotlivých funkciách – lineárna, kvadratická, linárna lomená, …