Nech pre funkcie f s definičným oborom D(f)) platí:
x ∈ D(f) a zároveň –x ∈ D(f)
V takom prípade rozlišujeme dva významné typy funkcií: párnu funkciu a nepárnu funkciu.
Párna funkcia:
Funkciu f nazývame párnou práve vtedy, keď pre každé x∈D(f) platí:
f(-x) = f(x)
Príklad 1:
Ktoré z daných funkcií sú párne?
- f: y = |x|
- g: y = x2
- h: y = |x – 1|
Riešenie:
a) Pri riešení nám postačuje určiť f(-x) a zistiť, či je rovné f(x).
Spomenieme si na absolútnu hodnotu:
|a| = a pre a≥0 … napr. |5| = 5
|a| = -a pre a<0 … napr. |-3| = -(-3) = 3
Výsledok je vždy kladné číslo.
Keďže predpis funkcie je y = |x|, tak musíme uvažovať dva prípady:
1. prípad: Overíme rovnosť pre x ≥ 0
f(x) = |x| = x … (v absolutnej hodnote je kladné číslo … odstránením absolútnej hodnoty sa nič nemení)
f(-x) = |-x| = -(-x) = x … (v absolutnej hodnote je záporné číslo … odstránením absolútnej hodnoty sa mení dané číslo na kladné)
V tomto prípade teda f(-x) = f(x)
2. prípad: Overíme rovnosť pre x < 0
f(x) = |x| = –x … (v absolutnej hodnote je záporné číslo … odstránením absolútnej hodnoty sa mení dané číslo na kladné)
f(-x) = |-x| = –x = x … (v absolutnej hodnote je kladné číslo … odstránením absolútnej hodnoty sa nič nemení)
Aj v tomto prípade teda f(-x) = f(x)
Môžeme teda povedať, že f(-x) = f(x) pre každé x∈D(f), teda funkcia je párna.
b) g: y = x2
g(x) = x2 pre každé x∈D(g)
g(-x) = (-x)2 = x2 pre každé x∈D(g) (vieme, že druhá mocnina ľubovoľného čísla je číslo nezáporné)
Opäť platí f(-x) = f(x) pre každé x∈D(f), teda funkcia je párna.
c) Keďže predpis funkcie je y = |x – 1|, tak musíme uvažovať dva prípady:
1. prípad: Overíme rovnosť pre x-1 ≥ 0, teda x ≥ 1
h(x) = |x-1| = x-1 … (v absolutnej hodnote je kladné číslo … odstránením absolútnej hodnoty sa nič nemení)
h(-x) = |-x-1| = -(-x-1) = x+1 … (v absolutnej hodnote je záporné číslo … odstránením absolútnej hodnoty sa mení dané číslo na kladné)
V tomto prípade teda h(-x) ≠ h(x) môžeme teda povedať, že funkcia nie je párna.
Nepárna funkcia:
Funkciu f nazývame nepárnou práve vtedy, keď pre každé x∈D(f) platí:
f(-x) = –f(x)
Príklad 2:
Ktoré z daných funkcií sú nepárne?
- f: y = x
- g: y = x2 – 1
- h: y = x – 1
Riešenie:
a) f(x) = x
f(-x) = –x = –f(x) … môžeme teda povedať, že f(-x) = –f(x) pre každé x∈D(f), teda funkcia je nepárna.
b) g(x) = x2 – 1
g(-x) = (-x2) – 1 = x2 – 1 ≠ –g(x) pre každé x∈D(g), teda funkcia nie je nepárna.
Všimnite si, že v tomto prípade g(-x) = g(x), teda funkcia je párna.
c) h(x) = x – 1
h(-x) = –x-1 = -(x+1) … (v absolutnej hodnote je kladné číslo … odstránením absolútnej hodnoty sa nič nemení)
f(-x) = |-x-1| = -(-x-1) = x+1 ≠ –h(x) pre každé x∈D(h), teda funkcia nie je nepárna.
Všimnite si, že v tomto prípade h(-x) ≠ h(x), teda funkcia nie je ani párna.
Ako zistíme, či je funkcia párna alebo nepárna, ak poznáme iba jej graf?
Stačí, keď si zopakujeme pojmy osová a stredová súmernosť.
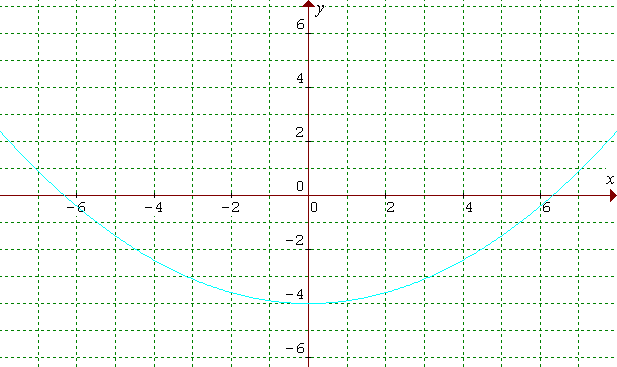
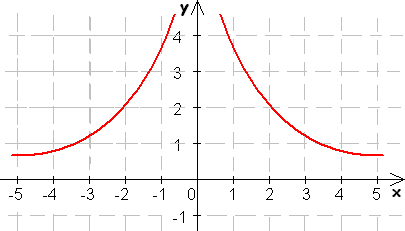
Funkcia je párna, ak jej graf je osovo súmerný podľa osi y.
Napríklad:
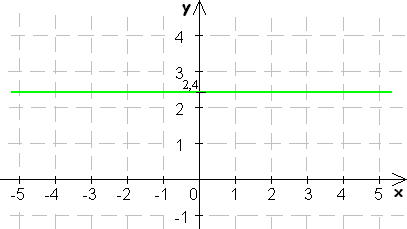
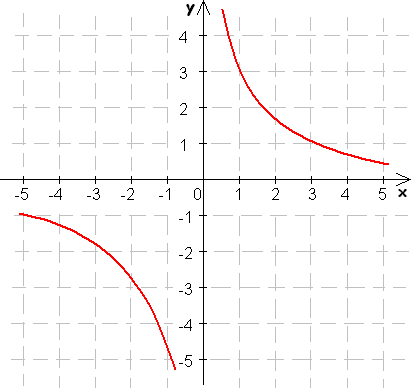
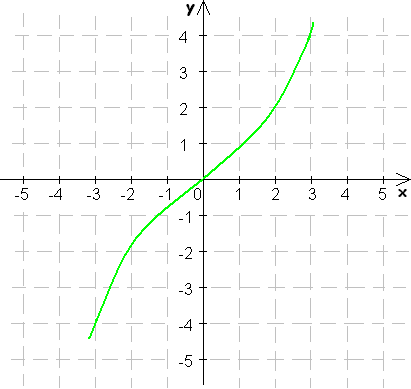
Funkcia je nepárna, ak jej graf je stredovo súmerný podľa bodu [0, 0].
Napríklad: