Výrok, axióma, definícia, úsudok, hypotéza, pravdivostná hodnota,
logické spojky, negácia, konjunkcia, disjunkcia, implikácia, ekvivalencia, výroková formula, tabuľka pravdivostných hodnôt, výroková forma, kvantifikátor (existenčný, všeobecný, aspoň, najviac, práve), negácie kvantifikovaných výrokov, matematická veta, existenčná veta, všeobecná veta, obrátená veta, obmenená veta, negácia vety, priamy dôkaz, nepriamy dôkaz, dôkaz sporom, dôkaz matematickou indukciou; množina, prvky množiny,
podmnožina, rovnosť množín, prienik, zjednotenie a rozdiel množín, Vennove diagramy, prázdna množina, disjunktné množiny, doplnok množiny, konečná a nekonečná množina.
je oznamovacia veta, o ktorej má zmysel hovoriť, či je pravdivá alebo nepravdivá.
Jednoduché výroky zvyčajne označujeme veľkými písmenami A, B, C, …
Výrokmi sú napr.:
- Barack Obama je prezidentom USA.
- Mount Everest (Sagarmatha) je najvyššou horou na svete.
- Londýn je hlavné mesto Mexika.
Výrokmi nie sú napr.:
- Sadni si!
- Utorok.
- Pôjdeš večer do kina?
je matematický výrok, ktorý považujeme za pravdivý a nedokazujeme ho. Pomocou axióm (nazývaných i postuláty) zavádzame jednotlivé matematické pojmy.
Sústava axióm musí byť:
- bezosporná, teda nie je možné z nej odvodiť výrok a zároveň i jeho negáciu;
- nezávislá, teda nie je možné pomocou jednej axiómy odvodiť inú axiómu;
- úplná, teda zo sústavy axióm je možné odvodiť pravdivosť či nepravdivosť ľubovoľného matematického výroku.
slúži na zavedenie nového matematického pojmu. Určí názov tohto pojmu a jeho charakteristické vlastnosti, pričom využíva skôr zavedené pojmy.
Príklady definícií:
- Mnohouholníkom nazývame konečnú postupnosť navzájom rôznych nekolineárnych bodov A1, …, An. Body A1, …, An nazývame jeho vrcholmi, úsečky A1A2, A2A3, …, AnA1 jeho stranami.
- Kružnicou k so stredom S a polomerom R nazývame množinu všetkých bodov v rovine, ktoré majú od pevného bodu S konštantnú vzdialenosť r.
- Vektorom nazývame množinu všetkých súhlasne orientovaných úsečiek rovnakej veľkosti.
je logická operácia resp. myšlienkový postup, pri ktorom sa z jedného alebo viacerých súdov (premisy), vyvodzuje nový súd (záver, dôsledok), ktorý logicky vyplýva z premís.
Napríklad:
- Súdy: V záhrade rastú samé ovocné stromy. V záhrade stojí košatá jabloň.
- Záver (dôsledok): Jabloň je ovocný strom.
je výrok, o ktorom nevieme rozhodnúť či je pravdivý alebo nepravdivý.
Napríklad:
- Každé párne číslo väčšie ako 2 je súčtom dvoch prvočísel. (tzv. Goldbachova hypotéza)
- Vo vesmíre sa nachádzajú aspoň 4 ľuďmi obývateľné planéty.
Pravdivý výrok označujeme znakom 1, nepravdivý výrok označujeme znakom 0. Hovoríme, že výrok má pravdivostnú hodnotu 1, (0). Označujeme p(A) = 1.
Napríklad:
- A: Číslo 312 je deliteľné číslom 6. p(A) = 1
- B: Obsah každého obdĺžnika vypočítame ako dvojnásobok súčtu jeho strán. p(B) = 0
sú ustálené slovné spojenia pomocou ktorých vytvárame zložené výroky z jednoduchých výrokov. Patria sem ∧, ∨, ⇒, ⇔.
výroku V je výrok, ktorého pravdivostná hodnota je opačná ako pravdivostná hodnota výroku V. Označenie: “ alebo ¬ (čítame „nie je pravda“,„neplatí“).
Teda ak p(V) = 1, tak p(V“) = 0 alebo ak p(V) = 0, tak p(V“) = 1.
Napríklad:
V: Rieka Dunaj ústí do Čierneho mora. p(V) = 1
V“: Rieka Dunaj neústi do Čierneho mora. p(V) = 0
Pozor: Napr. výrok „Každý trojuholník je rovnostranný.“ nie je negáciou výroku „Každý trojuholník je rovnoramenný.“
O tvorbe negácií sa môžete dozvedieť vo viacerých článkoch celku Matematická logika.
je spojenie dvoch výrokov pomocou logickej spojky a resp. a zároveň. Označenie: ∧
Napríklad:
- p: Americký raper 50 Cent bol 19.11.2007 na Slovensku.
- q: Techniku pre jeho vystúpenie malo priviezť 6 kamiónov.
- p ∧ q: Americký raper 50 Cent bol 19.11.2007 na Slovensku a techniku pre jeho vystúpenie malo priviezť 6 kamiónov.
Alebo:
- A: Číslo x je deliteľné tromi.
- B: Súčet cifier v čísle x je 21.
- A ∧ B: Číslo x je deliteľné tromi a súčet cifier v čísle x je 21.
Zložený výrok p∧q (konjunkcia) je pravdivý výrok, keď obidva výroky p, q sú pravdivé.
je spojenie dvoch výrokov pomocou logickej spojky alebo. Označenie ∨
Napríklad:
- p: V roku 1975 Jack Hawley vyvinul prvú guľôčkovú myš.
- q: Myš Logitech MediaPlay Cordless je zároveň diaľkovým ovládačom.
- p∨q: V roku 1975 Jack Hawley vyvinul prvú guľôčkovú myš alebo je myš Logitech MediaPlay Cordless zároveň diaľkovým ovládačom.
Alebo:
- A: Číslo 1234 je párne.
- B: Dvojnásobok čísla 1234 je nepárne číslo.
- A∨B: Číslo 1234 je párne alebo dvojnásobok čísla 1234 je nepárne číslo.
Zložený výrok p∨q (disjunkcia) je pravdivý, keď aspoň jeden z výrokov p, q je pravdivý (buď je pravdivý p, alebo q, alebo obidva).
je spojenie dvoch výrokov nesúce jazykový význam Ak ….., tak …... Označenie ⇒.
Napríklad:
- p: Ciferný súčet prirodzeného čísla X je deliteľný tromi.
- q: Prirodzené číslo X je deliteľné tromi.
- p⇒q: Ak ciferný súčet prirodzeného čísla X je deliteľný tromi, tak prirodzené číslo X je deliteľné tromi.
Zložený výrok p⇒q (implikácia) je pravdivý, keď nenastane prípad, že výrok p je pravdivý a výrok q je nepravdivý.
je spojenie dvoch výrokov pomocou logickej spojky práve vtedy resp. vtedy a len vtedy. Označenie: ⇔.
Napríklad:
- K: Funkcia f je zhora ohraničená na množine A.
- L: Existuje také reálne číslo k, že pre všetky x∈A platí: f(x)≤k.
- K⇔L: Funkcia f je zhora ohraničená na množine A práve vtedy, ak existuje také reálne číslo k, že pre všetky x∈A platí: f(x)≤k.
Zložený výrok p⇔q (ekvivalencia) je pravdivý, keď majú obidva výroky p, q rovnakú pravdivostnú hodnotu. (čiže sú oba pravdivé alebo sú oba nepravdivé)
Všeobecne symboly p, q, … reprezentujú nielen určité výroky, ale tiež výrokové premenné (premenné zastupujúce výroky).
Výrokovou formulou nazývame zápis, ktorý obsahuje výrokové premenné, logické spojky a zátvorky tak, že po dosadení ľubovolných výrokov za výrokové premenné dostaneme výrok.
Pomocou tabuľky pravdivostných môžeme zistiť, pre ktoré pravdivostné hodnoty výrokových premenných vznikne pravdivý alebo nepravdivý výrok.
Tabuľka pravdivostných hodnôt výrokových formulí základných zložených výrokov:
| P(p) | P(q) | P(p∧p) | P(p∨p) | P(p⇒p) | P(p⇔p) |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
Výroková forma je výraz obsahujúci premenné, po dosadení ktorých sa z neho stane výrok.
Napríklad:
Výroková forma je x2–2x>0, x∈R.
Všimnite si, že výroková forma sama o sebe nie je výrok (nemá zmysel uvažovať, či je platná alebo nie), až po vhodnom dosadení za premenné, napr. 22-2·2>0, z nej vzniká výrok.
Okrem dosadenia konštánt za výrokové premenné môžeme z výrokových foriem dostať výroky i použitím kvantifikátorov. Tzn. doplnením výrokovej formy údajom o počte resp. odhadom počtu konštánt, ktorých dosadením do výrokovej formy by sme dostali pravdivé výroky.
Použitím kvantifikátorov získavame tzv. kvantifikované výroky.
Kvantifikátory:
| Slovné spojenie | Význam |
|---|---|
| každý objekt (všetky) | ľubovoľný objekt z adnej množiny |
| aspoň jeden objekt | jeden alebo viac objektov |
| najviac jeden objekt | jeden alebo žiadny objekt |
| práve jeden objekt | jediný objekt (jeden a len jeden) |
| aspoň n objektov (n∈N, n>1) | n alebo viac objektov |
| najviac n objektov (n∈N, n>1) | n alebo menej objektov |
| práve n objektov (n∈N, n>1) | n objektov (ani viac ani menej) |
Základné kvantifikátory:
| Pomenovanie | Označenie | Čítame |
|---|---|---|
| Všeobecný kvantifikátor | ∀ | pre každé, pre všetky |
| Existenčný kvantifikátor | ∃ | existuje, pre spoň jedno, aspoň jedno |
| Kvantifikátor jednoznačnej existencie | ∃! | existuje práve jedno, pre práve jedno |
Príklady základných kvantifikovaných výrokov:
- Všeobecný výrok
- ∀ x ∈ Z; x2 ≥ 0 … pravdivý výrok
- ∀ x ∈ R; x3 < -1 … nepravdivý výrok
- Existenčný výrok
- ∃ x ∈ N; x2-2 = 0 … nepravdivý výrok
- ∃ x ∈ Z; x + 2 > -1 … pravdivý výrok
- Výrok o existencii a unicite
- ∃! x ∈ Z; x2 – 4 = 0 … nepravdivý výrok
- ∃! x ∈ N; (x-3)(x+2) = 0 … pravdivý výrok
Negácie kvantifikovaných výrokov
| Kvantifikovaný výrok | Negácia tohto výroku |
|---|---|
| Každý … je …. Všetky … sú … Každé p …. je … (p ∈ N; n > 1) |
Aspoň jeden … nie je … Aspoň jeden z p … nie je …(p ∈ N; n > 1) |
| Aspoň jeden … je … Aspoň p …. je … (p ∈ N; n > 1) |
Žiadny … nie je … Najviac p-1 … je …(p ∈ N; n > 1) |
| Najviac p … je …(p ∈ N; n > 1) | Aspoň p+1 … je …(p ∈ N; n > 1) |
| Práve jeden … je … Práve p …. je … (p ∈ N; n > 1) |
Žiadny … nie je … alebo aspoň dva … sú … Najviac p-1 … je … alebo aspoň p+1 … je …(p ∈ N; n > 1) |
| ∀x ∈ D: V(x) | ∃x ∈ D: ¬V(x) |
| ∃x ∈ D: V(x) | ∀x ∈ D: ¬V(x) |
je pravdivý matematický výrok, ktorý je možné logicky odvodiť z axióm, definícií a skôr dokázaných viet.
má tvar existenčného výroku ∃x ∈ D: V(x) („existuje také x patriace do D, že platí V(x)“)
má tvar všeobecného výroku ∀x ∈ D: V(x) („pre každé x patriace do D platí V(x)“)
Všeobecné vety majú často tvar implikácií ∀x∈D: A(x) ⇒ B(x), kde výroková forma A(x) je predpokladom vety, B(x) tvrdením vety.
Aby veta platila, je platnosť predpokladu A(x) postačujúcou podmienkou pre platnosť záveru B(x) a platnosť záveru B(x) je nutnou podmienkou pre platnosť predpokladu A(x) pre každé x∈D.
napr. ∀a ∈ N: 9|a => 3|a je všeobecná veta, kde 9|a stačí k tomu, aby aj 3|a, teda 9|a je v našom prípade postačujúca podmienka, ale 3|a nestačí k tomu aby aj 9|a (napr.3|12 ale 9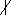 12), ale ak 9|a nutne musí aj 3|a. 3|a je nutná podmienka.
12), ale ak 9|a nutne musí aj 3|a. 3|a je nutná podmienka.
Pre všeobecnú vetu tvaru implikácie definujeme pojmy: obrátená veta, obmena vety, negácia vety.
Obrátená veta, obmenená veta, negácia vety
| Názov | Symbolický zápis | Pravdivostná hodnota | Príklad |
|---|---|---|---|
| všeobecná veta | ∀x ∈ D: A(x) ⇒ B(x) | ∀a ∈ N: 9|a ⇒ 3|a | |
| obrátená veta | ∀x ∈ D: B(x) ⇒ A(x) | môže a nemusí mať rovnakú pravd. hod. ako pôvodná veta |
∀a ∈ N: 3|a ⇒ 9|a |
| obmenená veta | ∀x ∈ D: ¬B(x) ⇒ ¬A(x) | ekvivalentná s pôvodnou vetou, čiže má rovnakú pravd. hodnotu |
∀a ∈ N: 3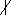 a ⇒ 9 a ⇒ 9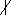 a a |
| negácia vety | ∀x ∈ D: A(x) ∧ ¬B(x) | opač. pravd. hodnota | ∀a ∈ N: 9|a ⇒ 3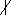 a a |
Dôkazy matematických viet
Dokazujeme vety tvaru A ⇒ B pomocou reťazca pravdivých implikácií.
Napríklad:
- Veta:
- Súčet dvoch párnych prirodzených čísel je párne prirodzené číslo.
- ∀x,y ∈ N: ak x = 2n ∧ y = 2k ⇒ x+y = 2v, (n,k,v ∈ N).
- Dôkaz:
- x = 2n ∧ y = 2k ⇒ x+y = 2n+2k = 2(n+k) = 2v a keďže 2v je určite párne číslo, tak veta platí.
Alebo:
- Veta:
- ∀n∈N: 2|n ⇒ 2|n2 (2|n znamená, že číslo n je deliteľné číslom 2)
- Dôkaz:
- 2|n ⇒ ∀k∈N: n = 2k ⇒ n2 = (2k)2 = 4k2 ⇒ n2 = 2∙2k2 ⇒ 2|n2
Namiesto implikácie A ⇒ B dokazujeme obmenenú vetu B“ ⇒ A“.
Napríklad:
- Veta:
- Ak x2 je párne číslo, tak aj x je párne číslo.
- ∀x∈N: 2|x2 ⇒ 2|x
- Dôkaz:
- Dokážeme priamo obmenenú vetu: ∀x∈N: 2
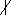 x ⇒ 2
x ⇒ 2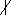 x2.
x2. - 2
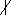 x ⇒ ∀k∈N: x=2k+1 ⇒ x2=(2k+1)2=4k2+4k+1=2(2k2+2k)+1=2m+1 (nepárne č.) ⇒ 2
x ⇒ ∀k∈N: x=2k+1 ⇒ x2=(2k+1)2=4k2+4k+1=2(2k2+2k)+1=2m+1 (nepárne č.) ⇒ 2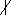 x2
x2
Namiesto konkrétneho výroku V dokazujeme jeho negáciu ¬V a pomocou reťazca implikácií získame logický spor. Zo sporu vyplýva, že negované tvrdenie ¬V neplatí, teda platí pôvodný výrok V.
Napríklad:
- Veta:
- V: ∀n ∈ N: 3|n ⇒ 3|n2
- Dôkaz:
- ¬V: ∀n ∈ N: 3|n ∧ 3
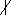 n2
n2 - ∀n∈N: 3|n ⇒ ∀k∈N: n = 3k ⇒ n2 = 9k2 ⇒ 3|n2 spor. Z toho vyplýva, že negácia vety neplatí, teda platí pôvodná veta.
Používame ho pri dokazovaní viet typu ∀n∈N, n > n0: V(n). Pozostáva z dvoch krokov a záveru:
- krok: Dokážeme, že veta platí pre n = n0, teda že platí V(n0)
- krok (tzv. indukčný): Dokážeme, že veta platí pre každé k > n0: ak platí V(k), tak platí aj V(k+1).
- V závere potvrdíme platnosť vety.
Napríklad:
- Veta:
- V(n): ∀n∈N: 31|5n+1 + 62n–1
- Dôkaz:
- 1.) k = 1 ⇒ 51+1 + 62∙1–1 = 25 + 6 = 31 ⇒ 31|51+1 + 62∙1–1
- 2.) Ideme dokázať implikáciu V(k) ⇒ V(k+1), teda
∀k∈N: 315k+1 + 62k–1 ⇒ ∀k∈N: 31|5(k+1)+1 + 62∙(k+1)–1
Červeným písmom som označil tzv. INDUKČNÝ PREDPOKLAD, o ktorom predpokladáme, že platí. Keď ho použijeme, tiež to vyznačím červeným písmom.
A ideme upravovať:
5(k+1)+1 + 62∙(k+1)–1 = 5k+2 + 62∙k+1 = 5∙5k+1 + 62∙62k–1 = 5∙5k+1 + 5∙62k–1 + 31∙62k–1 = 5∙(5k+1 + 62k–1) + 31∙62k–1 = 5∙31∙p + 31∙62k–1 = 31∙(5∙p + 62k–1) ⇒ ∀k∈N: 31|(5(k+1)+1 + 62∙(k+1)–1) čo bolo treba dokázať
je súbor navzájom rôznych (rozlíšiteľných) matematických alebo iných objektov. O každom z objektov sa musí dať rozhodnúť, či do danej množiny patrí alebo nie.
Množiny sa väčšinou označujú veľkými písmenami, napr. A, B, N a ich obsah (objekty) sa zapisujú do zložených zátvoriek. Napr. množinu A obsahujúcu objekty a, b zapíšeme A = {a, b}.
Objekty, ktoré patria do danej množiny nazývame prvky množiny. Obvykle ich označujeme malými písmenami x, y, c, …
Ak chceme vyjadriť, že prvok x je prvkom množiny M, tak zapíšeme x ∈ M a číta sa x je prvkom množiny M alebo x patrí množine M. Ak d nie je prvkom množiny B, tak zapíšeme d ∉ B. Každá množina je určená buď
- vymenovaním všetkých jej prvkov: B = {a, b, c, d},
- alebo určením charakteristických vlastností prvkov, ktoré do danej množiny patria: B = {x∈Z; 3 | x} je zápis množiny B, ktorej prvky sú celé čísla deliteľné číslom 3.
Množina A je podmnožinou množiny B práve vtedy, keď každý prvok množiny A je zároveň prvkom množiny B.
Symbolicky:
A ⊂ B ⇔ (∀x: x∈A ⇒ x∈B)
Napríklad:
- Množina {1,2,3} je podmnožinou množiny prirodzených čísel.
- Množina všetkých prirodzených čísel deliteľných číslom 9 je podmnožinou množiny všetkých čísel deliteľných číslom 3.
Množiny A a B sa rovnajú, keď každý prvok množiny A patrí množine B a každý prvok množiny B patrí množine A.
Symbolicky:
A = B ⇔ (∀x: x∈A ⇔ x∈B)
Napríklad:
- A = {∀x∈Z; |x|<2}; B = {-1;0;1}; A = B
- C je množina všetkých párnych prirodzených čísel deliteľných tromi; D je množina všetkých prirodzených čísel deliteľných šiestimi. C = D
Prienikom množín A a B nazývame množinu A ∩ B, ktorá obsahuje všetky prvky patriace súčasne do oboch množín A, B.
Napríklad:
- A = {2; 3; 4; 5}; B = {1; 3; 5; 7}; A ∩ B = {3; 5}
- C = {∀x∈Z; -2 ≤ x < 5}; D = N; C ∩ D = {1; 2; 3; 4}
Zjednotením množín A a B nazývame množinu A ∪ B, ktorá obsahuje prvky patriace aspoň do jednej z množín A, B, teda obsahuje prvky, ktoré patria do množiny A alebo do množiny B a okrem nich neobsahuje žiadne iné prvky.
Napríklad:
- A = {2; 3; 4; 5}; B = {1; 3; 5; 7}; A ∪ B = {1; 2; 3; 4; 5; 7}
- C = {∀x∈Z; -2 ≤ x < 5}; D = N; C ∪ D = {…; -2; -1; 0; 1; 2; 3; 4}
Rozdielom množín A a B nazývame množinu A – B (A \\ B), ktorá obsahuje tie prvky množiny A, ktoré súčasne
nepatria do množiny B.
Napríklad:
- A = {2; 3; 4; 5}; B = {1; 3; 5; 7}; A – B = {2; 4}
- C = {∀x∈Z; -2 ≤ x < 5}; D = N; C – D = Z0–
Na názornú predstavu množín, množinových vzťahov a operácií medzi množinami sa používajú ich grafické znázornenia v rovine, tzv. množinové diagramy. Základná množina Z sa znázorňuje spravidla obdĺžnikom a jej podmnožiny A, B, … ako kruhy alebo iné zvyčajne oválne obrazce vnútri obdĺžnika. Tieto grafické znázornenia sa nazývajú Vennove diagramy.
K znázorneniu množín reálnych čísel sa zvyčajne používa číselná os.
Pozrite výklad k téme Množiny.
je množina, ktorá neobsahuje žiadne prvky. Zapisujeme ju pomocou symbolu ∅ alebo {}.
Napríklad:
- A = ∅ B = {};
Ak je prienikom množín A, B prázdna množina (A∩B=∅), nazývame množiny A, B
disjunktnými.
Napríklad:
- A = {2; 3; 4; 5}; B = {6; 7};
- C = {∀x∈Z; -2 ≤ x < 5}; D = {∀x∈N; x > 5}
Doplnok množiny A vzhľadom na množinu U je množina A“U všetkých prvkov množiny U, ktoré
nepatria do množiny A.
Napríklad:
- A = {2; 3; 4; 5}; B = {1; 2; 3; 4; 5; 6; 7}; A“B = {1; 6; 7}
Každú množinu, ktorá obsahuje konečný počet prvkov nazývame konečnou množinou. Konečný počet prvkov je daný prirodzených číslom resp. nulou, čiže i prázdna množina je konečnou množinou.
Napríklad:
- A = {2; 3; 4; 5}; je konečnou množinou, obsahuje 4 prvky
Množinu, ktorá nie je konečnou nazývame nekonečná.
Napríklad:
- B = {∀x∈R: |x|≤3}; je nekonečnou množinou, obsahuje nekonečne veľa prvkov
