Graf funkcie, funkcia daná analyticky, graficky, vymenovaním usporiadaných dvojíc
Graf funkcie:
V rovine si zvolíme pravouhlú sústavu súradníc so začiatkom O a osami x, y. Pre všetky x∈D(f) priradíme každej usporiadanej dvojici (x, f(x)) bod v rovine so súradnicami x, y=f(x).
Napríklad funkcia f je daná ako množina usporiadaných dvojíc
{(-6,5; 2), (-2; -1,5), (-1; 2,5), (3,5; -2), (4; 3)}.
Graf tejto funkcie bude vyzerať nasledovne:
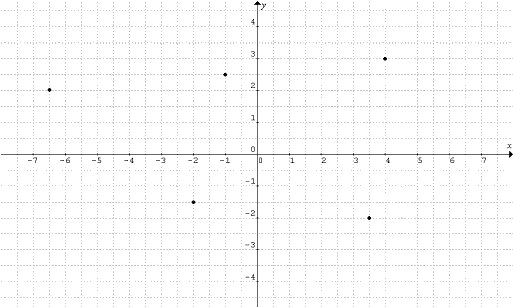
Bližšie ku grafom jednotlivých funkcií sa dozviete v rámci tém venovaných konkrétnym funkciám.
Funkcia môže byť daná
a) analyticky – vzorcom, t.j. rovnicou v tvare y = f(x), kde f(x) je výraz s premennou x, napr. y = 2x – 7 alebo y = x + x – 3
b) graficky – grafom funkcie
c) vymenovaním usporiadaných dvojíc – spravidla vo forme tabuľky. Tento spôsob je použiteľný jedine pre funkcie, ktorých definičným oborom je konečná množina.
Príklad 1:
Je daná množina usporiadaných dvojíc reálnych čísel funkciou?
Vedeli by sme zistiť aj to, či graf na obrázku je grafom funkcie?
Niektorí áno, niektorí nie. Ja vám poradím malú fintu.
Skúste v myšlienkach posúvať y-ovú os po obrázku a v prípade, že vždy pretne graf v danom okamihu len na jednom mieste, tak je grafom funkcie. V opačnom prípade nie je grafom funkcie.
Pozorne sledujte nasledovnú ukážku (kliknutím na Zisťuj):
Všimnite si, že v okamihu, keď os y pretína graf na dvoch a viacerých miestach súčasne, vykresľuje sa červenou farbou na osi x interval, ktorý reprezentuje všetky hodnoty premennej x, ktorým je priradená viac ako jedna hodnota premennej y, čiže daný graf nie je grafom funkcie.
Príklad 2:
Príklad 3:
Určte definičné obory a obory funkčných hodnôt daných funkcií:
a) f1: A = {[1; 6], [3; 4],[5; 6],[7; 4],[9; 6],[11; 4]}
b) f2: B = {[1; 6], [3; 8],[5; 10],[7; 12],[9; 14],[11; 16]}
c) f3: C = {[x,y]∈RxR; y = 2x + 1}
d) f4: D = {[x,y]∈RxR; y = |2x + 1|}
Riešenie:
a) D(f1)={1;3;5;7;9;11}; H(f1)={4;6}
b) D(f2)={1;3;5;7;9;11}; H(f2)={6;8;10;12;14;16}
c) D(f3)=R; H(f3)=R
d) D(f4)=R; H(f4)=<0; ∞)
Možno sa teraz pýtate: „A čo v prípade, ak je funkcia daná analyticky? Je to tiež tak jednoduché?“
Pre vás je dôležité uvedomiť si, že zatiaľ si budete na funkcii danej analyticky všímať hlavne dve veci:
Ak je v predpise menovateľ, v ktorom sa nachádza premenná, tak
MENOVATEĽ SA NESMIE ROVNAŤ NULE
a v prípade, ak sa v predpise funkcie nachádza odmocnina s párnym odmocniteľom, tak
POD ODMOCNINOU S PÁRNYM ODMOCNITEĽOM NESMIE BYŤ ZÁPORNÉ ČÍSLO.
Príklad 4:
Určte definičné obory a obory funkčných hodnôt daných funkcií:
a) f1: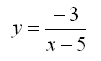 
b) f2: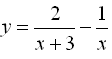 
c) f3: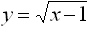 
d) f4: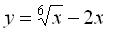 
e) f5: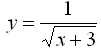 
Riešenie:
a) D(f1) = R - {5}, vychádza z podmienky (x-5)≠0
b) D(f2) = R - {0;3}, vychádza z podmienky (x-3)≠0 ∧ x≠0
c) D(f3) = <1;∞), vychádza z podmienky (x-1)≥0
d) D(f4) = <0;∞), vychádza z podmienky x≥0
e) D(f5) = (-3;∞), vychádza z podmienky (x+3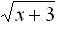)≥0 ∧ 
≠ 0
Rovnosť funkcií
O dvoch funkciách f a g hovoríme, že sú si rovné práve vtedy, ak D(f) = D(g) a v každom bode x tohto definičného oboru je f(x) = g(x). Zapisujeme f = g.
V prípade rôznych funkcií píšeme f ≠ g.
Napríklad funkcie g: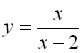 
a h: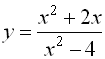 
sú rôzne, lebo D(g)≠D(h) (D(g)=R-{2}; D(h)=R-{-2;2}), pre x≠-2 platí g(x)=h(x).
Funkcie f: y=x2 a g: y=|x|2 sú rovné, lebo D(f)=D(g)=R a pre každé x∈R platí: f(x)=)g(x).