Obsah článku:
Uhly môžeme násobiť a deliť numericky alebo graficky. Poďme sa najskôr pozrieť na násobenie uhlov dvomi.
Násobenie uhlov dvomi
Numerické násobenie uhlov
Násobiť dvomi môžeme tie uhly, ktorých veľkosť je menšia alebo rovná 180°. Násobíme jednoducho tak, že osobitne vynásobíme stupne a osobitne minúty, ak je výsledný počet minúť väčší ako 60, tak odpočítame 60 minút od minút a k stupňom pripočítame 1°.
Poďme sa radšej pozrieť spoločne na konkrétne príklady.
Príklad č. 1: Vynásobte dvomi nasledovné uhly: 12°, 27°, 124°, 12°13´, 122°37´.
Riešenie:
12° . 2 = 24°
27° . 2 = 54°
124° . 2 = 248°
12°13´ . 2 = 24°26´ – iba jednoducho vynásobíme stupne aj minúty
122°37´ . 2 = 244°74´ (po vynásobení je počet minút > 60, preto musíme od minút odpočítať 60 a k stupňom 1 pripočítať) = (244+1)°(74-60)´ = 245°14´
[adinserter block=“2″]Grafické násobenie uhlov dvomi
Grafické násobenie uhlov dvomi najlepšie pochopíte pri konkrétnom príklade.
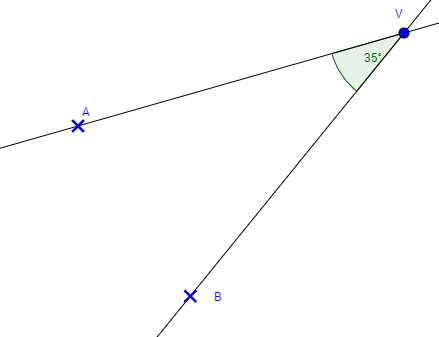
Príklad 2: Daný je uhol α = 35°. Graficky zostrojte dvojnásobok uhla α.
Riešenie:
1. Narysujeme uhol α = 35°.
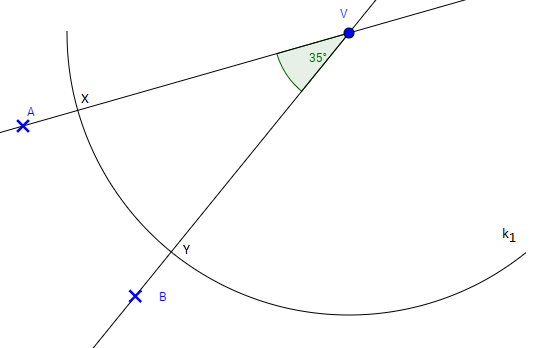
2. Zostrojíme kružnicový oblúk k1 so stredom v bode V a ľubovoľným polomerom. Body X, Y sú prieniky ramien uhla a kružnice k1.
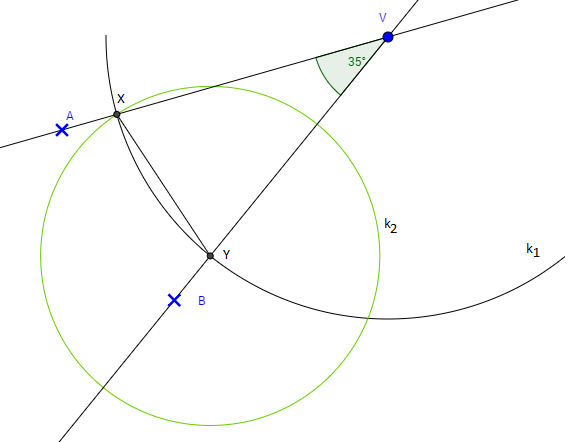
3. Zostrojíme kružnicu k2, so stredom v bode Y a polomerom |YX|.
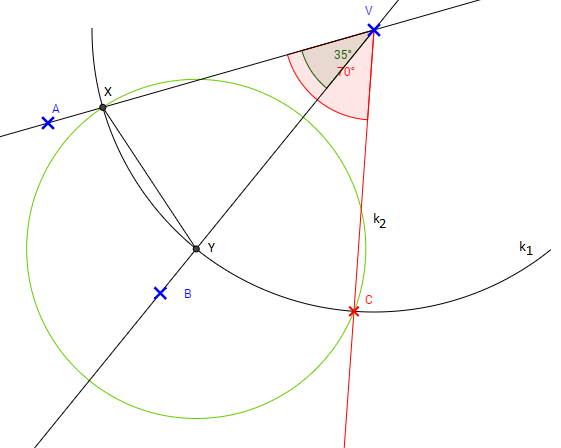
4. Bod C je druhý z priesečníkov kružníc k1 a k2. Bodom C vedieme polpriamku VC. Vzniknutý uhol AVC je dvojnásobkom uhla AVB.
Delenie uhlov dvomi
Numerické delenie uhlov
Uhol delíme dvomi tak, že osobitne vydelíme stupne a osobitne minúty.
Pozrime sa na konkrétne príklady.
Príklad č. 3: Vydeľte dvomi nasledovné uhly: 36°, 27°, 128°, 12°13´.
Riešenie:
36° : 2 = 18°
27° : 2 = 13,5° = (13+0,5)° = 13° + (0,5 . 60)´ = 13°30´
128° : 2 = 64°
12°13´ : 2 = 6°6,5´ = 6°(6+0,5)´ = 6°6´(0,5 . 60)´´ = 6°6´30´´
Grafické delenie uhlov dvomi
Uhol delíme graficky dvomi tak, že zostrojíme os daného uhla, ktorý rozdelí uhol na dve polovice.
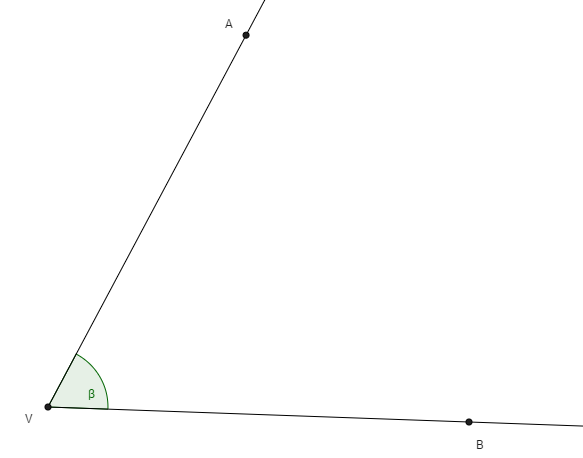
Príklad 4: Daný je uhol β = 64°. Zostrojte uhol, ktorý bude polovicou uhla β.
Riešenie:
1. Narysujeme uhol β = 64°.
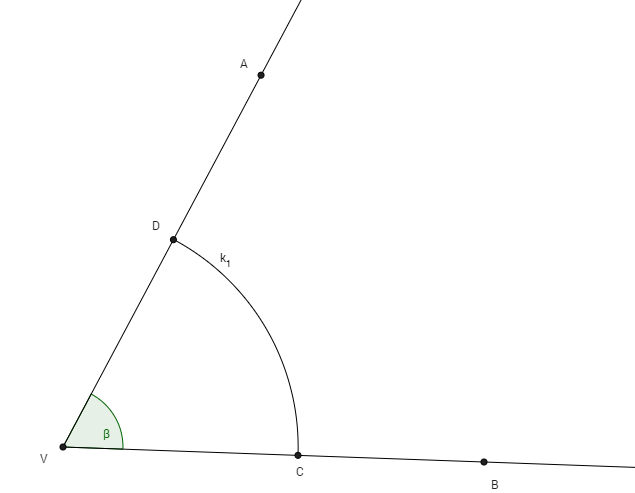
2. Zostrojíme kružnicový oblúk k1 so stredom v bode V a ľubovoľným polomerom. Body C, D sú prieniky ramien uhla a kružnice k1.
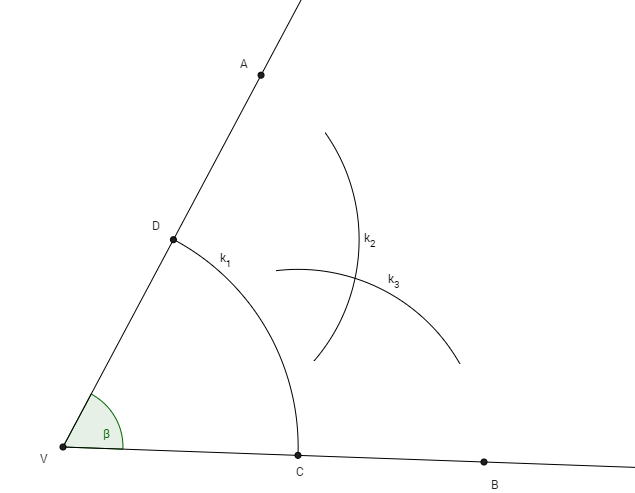
3. Zostrojíme kružnicu k2 so stredom v bode D a polomerom väčším ako |CD| a kružnicu k3 so stredom v bode C a rovnakým polomerom ako má kružnica k2.
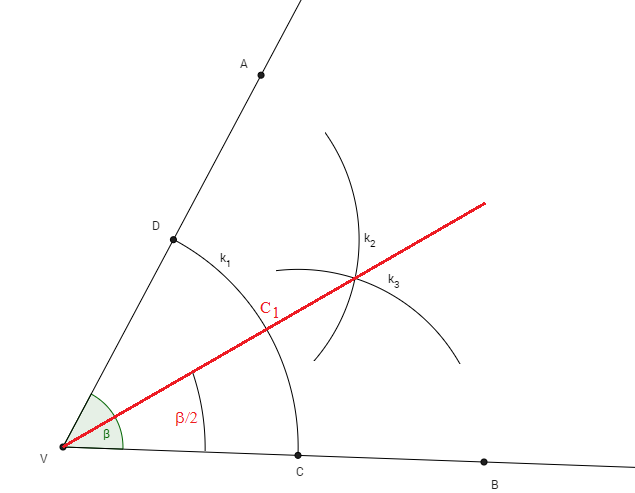
4. Prienikom kružníc k2 a k3 je bod C1. Vzniknutý uhol AVC1 je polovicou uhla β.