Rozširovanie a krátenie zlomkov, úprava zlomkov na základný tvar.
Pri vysvetľovaní delenia dvoch prirodzených čísel sme sa dozvedeli, že výsledok – podiel sa nezmení, ak delenca i deliteľa vynásobíme tým istým číslom rôznym od nuly.
Teda 4:5 = 8:10 = 40:50 = …
Keďže zlomok je „len“ iný zápis delenia, tak to isté platí i pri zlomkoch. Hovoríme o tzv. rozširovaní zlomku.
Teda 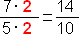 , takže takýmto rozširovaním by sme získali „nekonečne veľa“ zlomkov s rovnakou hodnotou.
, takže takýmto rozširovaním by sme získali „nekonečne veľa“ zlomkov s rovnakou hodnotou.
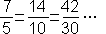
Príklad 1:
Rozšírte dané zlomky číslom uvedeným v zátvorke:
a) 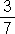 … (3)
… (3)
b) 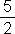 … (7)
… (7)
c) 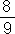 … (5)
… (5)
Riešenie:
a) 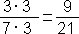
b) 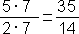
c) 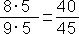
Pýtate sa na použitie rozširovania zlomkov?
Rozširovanie zlomkov môžeme použiť napr. pre rýchlejšie určenie hodnoty zlomku (nemusíme krvopotne deliť čitateľa menovateľom, ale stačí vhodne zlomok rozšíriť).
Napr. 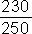 rozšírime číslom 4, dostaneme tak zlomok
rozšírime číslom 4, dostaneme tak zlomok 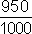 a dostaneme desatinný zlomok, ktorý vieme zapísať v tvare desatinného čísla 0,95 (bližšie pozrite Poznávame desatinné čísla).
a dostaneme desatinný zlomok, ktorý vieme zapísať v tvare desatinného čísla 0,95 (bližšie pozrite Poznávame desatinné čísla).
Ďalším príkladom môže byť uľahčenie riešenia príkladov typu:
Koľko minút je 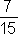 hodiny?
hodiny?
Vieme, že 1 hodina = 60 minút, čiže celok potrebujeme rozdeliť na 60 častí. Z toho vyplýva, že menovateľ potrebujeme rozšíriť na 60 a čitateľ bude predstavovať počet častí, ktoré sme zobrali, čiže počet minút.
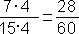 , čiže
, čiže 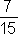 hodiny je 28 minút. Samozrejme, keď vieme, čo robiť, ide nám to rýchlejšie.
hodiny je 28 minút. Samozrejme, keď vieme, čo robiť, ide nám to rýchlejšie.
Tak ako môžeme násobiť čitateľa i menovateľa zlomku tým istým číslom a hodnota sa nezmení, platí to i opačne. Hodnota zlomku sa nezmení, ak čitateľa i menovateľa vydelíme tým istým číslom rôznym od nuly.
Hovoríme o krátení zlomku.
Krátenie zlomkov má zmysel najmä v zjednodušení daného zlomku pri zachovaní jeho hodnoty. Význam krátenia zlomkov oceníme najmä pri úpravách výrazov, riešení rovníc a pod.
Pozrime sa napr. na zlomok 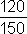 . Jedným zo spoločných deliteľov čísel 120 a 150 (bližšie pozrite Znaky deliteľnosti a Určenie všetkých deliteľov prirodzeného čísla, najväčší spoločný deliteľ) je číslo 5. Vydeľme teda čitateľa i menovateľa číslom 5.
. Jedným zo spoločných deliteľov čísel 120 a 150 (bližšie pozrite Znaky deliteľnosti a Určenie všetkých deliteľov prirodzeného čísla, najväčší spoločný deliteľ) je číslo 5. Vydeľme teda čitateľa i menovateľa číslom 5.
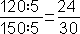
Získali sme zlomok 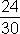 . Tento zlomok by sme mohli samozrejme krátiť ďalej. Veď sa pozrite:
. Tento zlomok by sme mohli samozrejme krátiť ďalej. Veď sa pozrite:
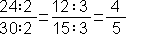
A čo so zlomkom 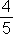 ? Je možné tento zlomok krátiť ďalej? Nie. Lebo čísla 4 a 5 sú nesúdeliteľné, čiže nemajú spoločného deliteľa. V takomto prípade hovoríme, že sme zlomok upravili na základný tvar.
? Je možné tento zlomok krátiť ďalej? Nie. Lebo čísla 4 a 5 sú nesúdeliteľné, čiže nemajú spoločného deliteľa. V takomto prípade hovoríme, že sme zlomok upravili na základný tvar.
